Зеркала

ЗАКОН ПРЕЛОМЛЕНИЯ: луч падающий, луч преломленный и перпендикуляр к поверхности раздела, восстановленный из точки падения луча, лежат в одной плоскости – плоскости падения. Отношение синуса угла падения к синусу угла отражения равно отношению скоростей света в обеих средах.

ЗАКОН ОТРАЖЕНИЯ: луч падающий, луч отраженный и перпендикуляр к поверхности раздела, восстановленный в точке падения луча, лежат в одной плоскости, называемой плоскостью падения; угол падения равен углу отражения.

Законы отражения и преломления света

Получим с помощью принципа Ферма законы отражения и преломления света. Пусть свет падает из точки А в точку В, отразившись от поверхности MN. Геометрическая длина произвольного пути 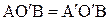(т.является зеркальным отражением т. A).

<.

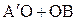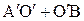Но .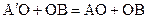

Сделав дополнительные построения пунктирными линиями видим, что наименьшей длиной обладает путь луча, отразившегося в т. О.

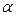– угол падения,

– угол отражения.

<

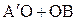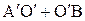
Но,

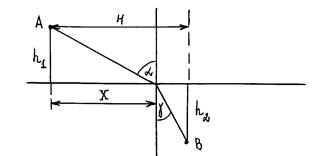Рассмотрим случай, когда точки А и В лежат в разных средах. Время прохождения луча от точки А до точки В:

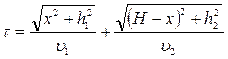
Учитывая принцип Ферма, исследуем на экстремум величину :

.

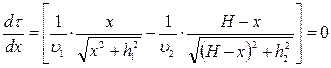Из рисунка видно, что полученную формулу можно преобразовать:

.

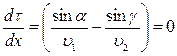Отсюда:

, но (с – скорость света в вакууме, - скорость света в среде с показателем преломления n (– абсолютный показатель преломления). С учетом этого:

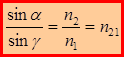, где 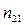– относительный показатель преломления второй среды относительно первой среды.

Можно записать и так:

.

Из закона преломления, применяемого для случая >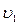, следует:

, т.к. >, .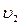

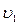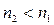
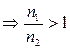, возможно, что .

, т. е. угол преломления равен 90^о, при этом преломленный луч скользит по границе раздела. В этом случае угол падения называют – предельным углом. При дальнейшем увеличение угла падения проникновение луча вглубь второй среды прекращается и наступает полное отражение.

Явление полного внутреннего

отражения используется в волоконной

оптике при создании световодов –

тонких прозрачных волокон.

Для понимания основных закономерностей в явлениях отражения наиболее целесообразно рассмотреть отражение в плоских и сферических зеркалах. Зеркала для оптических систем изготовляются в виде плоскостей или сфер из стекла, на поверхность которых наносится испарением в вакууме или химическим путем слой металла (серебра, алюминия, меди и др.), дающих высокий коэффициент отражения света. Вместе с этим применяется способ изготовления зеркал из цельного куска металла, например, алюминия. Изобразим на рисунке ход лучей при отражении света от плоской поверхности S:

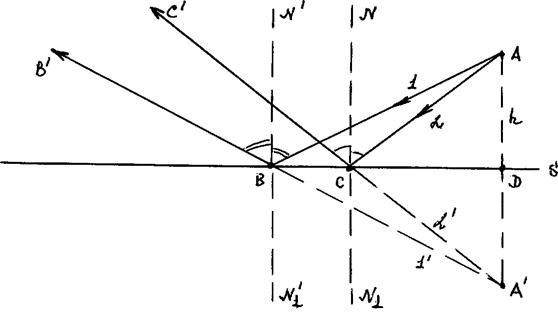
Свет идет из точечного источника А. и – нормали к поверхности S. Из закона отражения света следует: , 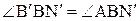. Лучи и 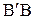являются отраженными. Продолжим луч 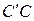до пересечения с продолжением высоты h вниз. Из построения следует: . Значит треугольники ACD и равны между собой. Отсюда следует, что 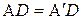. Это же заключение можно было сделать из рассмотрения луче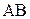й и . Доказано: после отражения от плоского зеркала лучей, исходящих из точечного источника, они идут так, как будто вышли из мнимого источника, находящегося позади зеркала на перпендикуляре к его плоскости, равном расстоянию действительного источника от плоскости зеркала. В рассмотренном случае таким мнимым источником является точка .

Изображение произвольного предмета может быть определено путем построения изображения точек, из которых состоит предмет.

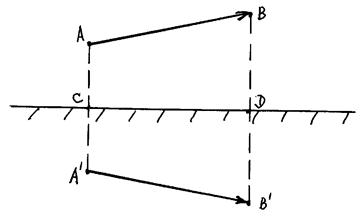
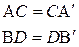
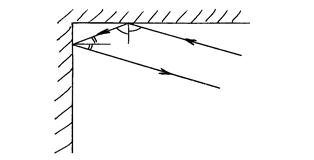
Плоские зеркала находят широкое применение в самых разнообразных оптических приборах. Важным применением плоских зеркал является поворот луча света точно в обратном направлении. Это достигается с помощью уголкового отражения, представляющего собой совокупность трех плоских зеркал, поставленных под прямым углом друг к другу.

Рассмотрим теперь явление отражения света от сферического зеркала. Вначале рассмотрим отражение от вогнутого зеркала S.

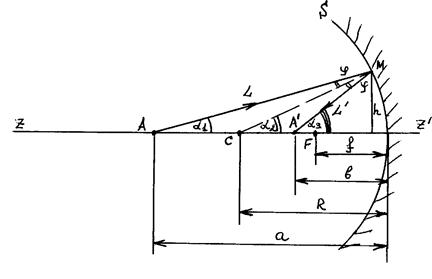Введем существенное ограничение: будем рассматривать только прохождение лучей, незначительно удаленных от оси симметрии , которая называется оптической осью зеркала (аналогично оптической оси линзы, оптической системы). Также лучи называют параксиальными лучами, а совокупность явлений в оптических системах при таком ходе лучей получила название параксиальная оптика. Из-за малости угла наклона при данном рассмотрении можно значение тангенсов и синусов этих углов заменить значениями самих углов.

Точка является пересечением лучей и , отраженных от зеркала, и представляет собой изображение точки А. Введем обозначения:

О – вершина зеркала,

a = АО – расстояние от вершины зеркала до источника света,

b = 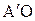– расстояние от вершины зеркала до изображения источника,

R = OC – радиус кривизны зеркала (совпадает с нормалью),

f = OF – фокусное расстояние,

h – расстояние т. М от оптической оси.

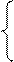Будем считать отрезки вправо от точки О и вверх от оптической оси положительными, а влево и вниз – отрицательными. Из чертежа видно:

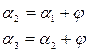Преобразуем:

Откуда: .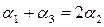

Ввиду малости углов: , , .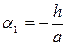

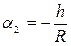После подстановки:

.

Если , то 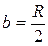. Тогда F, в которой получается изображение в этом случае называется главным фокусом зеркала (или просто фокусом).

Расстояние f от т. F до вершины О зеркала S называется фокусным расстоянием, причем:

.

Таким образом, падающие на зеркало параллельные лучи после отражения собираются в его фокусе.

– формула зеркала, f < 0, R < 0, фокус F действительный.

Рассмотрим теперь изображение в выпуклом зеркале.

Из Δ AMС:

;

Δ :

Отсюда:

Для углов: ,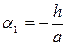

, .

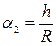Подставляя, получим: 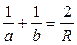. Формула для выпуклого зеркала такая же, как и для вогнутого. Если , то .

Точка F является мнимым фокусом выпуклого зеркала (f > 0, R > 0). После подстановки:

– формула зеркала.

Линейным увеличением зеркала называют отношение линейных размеров изображения к линейным размерам предмета:

.

Дата добавления: 2013-12-13