Статический метод исследования устойчивости стержневых систем

Методы исследования устойчивости

Основными методами исследования устойчивости являются:

1) статический метод;

2) динамический метод;

3) энергетический метод.

Сущность статического метода заключается в том, что для возможного критического состояния записывается уравнение возможного вида деформированной оси элемента. Из характеристических уравнений деформирования определяются те значения Р_кр внешних сил, при которых возможна новая форма равновесия.

Применяя динамический метод, составляют уравнения частоты собственных колебаний стержня сжатого силой Р и определяют то значение силы Р_кр, при котором частота собственных колебаний будет равна нулю.

Энергетический метод основан на принципе Дирихле, согласно которому если система находится в состоянии устойчивого равновесия, то ее полная потенциальная энергия минимальна Э = min; если система находится в неустойчивом состоянии, то ее потенциальная энергия максимальна Э = max, а если система находится в безразличном состоянии, то разность приращений энергий двух соседних возможных состояний равна нулю, т.е.

Э = DU - DT =,

где DU - приращение потенциальной энергии внутренних сил;

DТ - внешних сил.

Или: DU = DТU

Записывая выражения приращений потенциальной энергии внешних и внутренних сил, на любом возможном состоянии, из равенства DU = DТ определяют Р_кр.

При исследовании статическим методом, рассматриваемой системе задается отклоненная форма равновесия (допускаемая имеющимися связями), совпадающая с новой ожидаемой формой системы после потери устойчивости, и определяются значения нагрузок, способных удержать систему в новой форме равновесия.

Обычно считают, что отклоненная форма равновесия бесконечно близка к исходной, а координаты граничных условий принимаются по исходному состоянию. Определенные на основе таких предпосылок нагрузки считаются критическими. Они соответствуют безразличному равновесию между исследуемым состоянием и бесконечно близким к нему.

Покажем применение этого способа на примере стержня постоянного сечения опертого по концам, критическая сила для которого по формуле Эйлера

¦

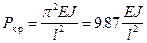
EI P

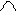
а)

i

P¦

б) M_прод.

P=1

в) M

½ i/4 ½

Зададим стержню бесконечно малое перемещение, которое будем определять одним параметром - прогибом f. Эпюра 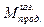от силы Р дана на рис. б. Найдем перемещение f.

Если приближенно эпюру принять в виде треугольника:

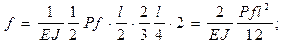
или

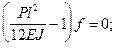
в момент потери устойчивости f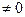, тогда

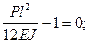отсюда: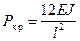

Если предположить, что эпюра моментов от силы Р определяется параболой, то

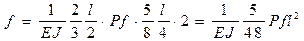
или

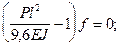
отсюда:

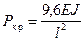более близко к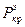

Дата добавления: 2014-01-04