Понятие несобственного интеграла

Лекция 26. Несобственные интегралы

Зададим на отрезке функцию 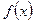. Допустим, что она интегрируема на любом отрезк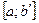е , где , и неограничена в окрестности точки b. Тогда её интеграл на не может существовать (так как интегрируемая по Риману функция на необходимо ограничена). Однако может случиться, что существует конечный предел . Если это так, то этот предел называют несобственным интегралом от функции 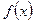на отрезке :

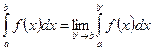. (26.1)

В таком случае говорят, что интеграл сходится. В противном случае говорят, что он расходится или не существует как несобственный риманов интеграл.

Допустим теперь, что функция 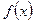задана на луче 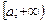и интегрируема на любом конечном отрезк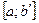е , где 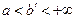. Если существует предел , то он называется несобственным интегралом от функции 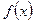на луче :

.

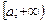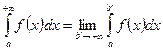Дата добавления: 2014-01-04