Круг сходимости

Пользуясь данной в предыдущем пункте теоремой Абеля, можно выяснить структуру области сходимости про­извольного степенного ряда. Во-первых, как мы уже знаем, суще­ствуют степенные ряды, область сходимости которых состоит из одной нулевой точки. Во-вторых, существуют степенные ряды, схо­дящиеся во всякой точке плоскости, т.е. имеющие областями схо­димости всю плоскость. На основании теоремы Абеля такие ряды должны абсолютно сходиться во всякой точке плоскости. Возьмём, например, ряд .

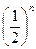Каково бы ни было , модуль общего члена этого ряда будет меньше, чем , начиная с 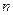, для которого .

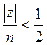Итак, все члены нашего ряда, кроме конечного числа первых членов, по модулям меньше соответствующих членов бесконечно убывающей прогрессии и 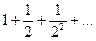, следовательно, рассматриваемый ряд абсолютно сходится при всяком .

Наконец, к третьему типу мы отнесём всякий степенной ряд, не принадлежащий ни к первому, ни ко второму типу. Исследуем область сходимости ряда последнего вида. Такой ряд имеет, с одной сто­роны, точки сходимости, отличные от нулевой точки, а с другой стороны, он имеет точки расходимости. Проведём из нулевой точки произвольную полупрямую и отметим на ней какую-нибудь точку сходимости ряда, отличную от нулевой точки, и какую-нибудь точку расходимости нашего ряда. Так как наш ряд принадлежит к третьему типу, то на основании теоремы Абеля точки и на полупрямой существуют. Обозначим через 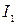отрезок 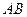. Разделим отрезок 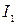пополам, и пусть есть его середина. Возможно одно из двух: либо в точке ряд сходится, либо расходится. В первом случае за второй отрезок 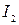примем 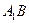, во втором случае . 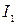Подобно отрезку отрезок 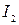имеет левым своим концом точку сходимости ряда, а правым – точку расходимости ряда. Затем снова делим пополам отрезок 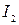, и если его середина есть точка сходи­мости ряда, то за отрезок 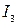принимаем правую его половину, а если середина отрезка 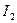есть точка расходимости ряда, то за отрезок 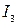принимаем левую половину отрезка 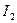Продолжая этот процесс не­ограниченно, получим бесконечную последовательность отрезков 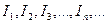таких, что каждый отрезок принадлежит пре­дыдущему, причем длина отрезка , равна , стремится к нулю, когда 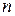неограниченно возра­стает. Кроме того, отметим, что всякий отрезок имеет своим левым концом точку сходимости ряда, а правым – точку расходимости ряда. На основа­нии принципа вложенных отрезков существует точка, общая всем отрезкам обозна­чим её через .

Проведя через точку окружность с центром в нулевой точке (Рис.40.2.), мы видим, что данный ряд абсолютно сходится во всякой точке, лежащей внутри этой окружности. действительно, пусть – любая точка, расположенная внутри проведённой окружности. Выберем на радиусе 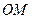внутреннюю точку 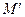, служащую левым концом отрезка , так, чтобы 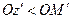. Так как в точке 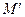дан­ный ряд сходится, то по теореме Абеля он будет абсолютно сходя­щимся в точке . Во всякой точке 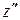, лежащей вне построений окружности, данный ряд расходится. В самом деле, выберем вне радиуса 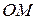на луче 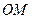точку , служащую правым концом отрезка , так, чтобы 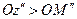. Так как в точке ряд расхо­дится, то по теореме Абеля он будет расходящимся и в точке 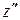. Полагая 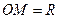, мы можем всё сказанное резюмировать в таких словах:

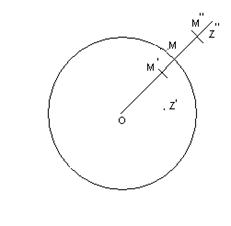
Рис. 40.2.

Дата добавления: 2014-01-04