Пример применения MATLAB

Интегральные теоремы

Теорема о градиенте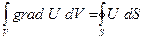

Теорема о дивергенции

Теорема о роторе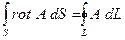

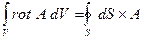
Задача.

Дано: В объёме тетраэдра скалярное и векторное поля изменяются по линейному закону. Координаты вершин тетраэдра заданы матрицей вида [ x ₁, y ₁, z ₁; x ₂, y ₂, z ₂; x ₃, y ₃, z ₃; x ₄, y ₄, z ₄]. Значения скалярного поля в вершинах заданы матрицей [Ф₁; Ф₂; Ф₃; Ф₄]. Декартовы компоненты векторного поля в вершинах заданы матрицей [ F _{1 x} , F _{1 y} , F _{1 z} ; F _{2 x} , F _{2 y} , F _{2 z} ; F _{3 x} , F _{3 y} , F _{3 z} ; F _{4 x} , F _{4 y} , F _{4 z} ].

Определить в объёме тетраэдра градиент скалярного поля, а также дивергенцию и ротор векторного поля. Составить для этого функцию MATLAB.

Решение. Ниже приведён текст m-функции.

% grad_div_rot - Вычисление градиента, дивергенции и ротора... в объёме тетраэдра

% [grad,div,rot]=grad_div_rot(nodes,scalar,vector)

% ВХОДНЫЕ ПАРАМЕТРЫ

% nodes - матрица координат вершин тетраэдра:

% строкам соответствуют вершины, столбцам - координаты;

% scalar - столбцовая матрица значений скалярного поля в вершинах;

% vector - матрица компонентов векторного поля в вершинах:

% строкам соответствуют вершины, столбцам - декартовы компоненты.

% ВЫХОДНЫЕ ПАРАМЕТРЫ

% grad - матрица-строка декартовых компонентов градиента скалярного поля;

% div - значение дивергенции векторного поля в объёме тетраэдра;

% rot - матрица-строка декартовых компонентов ротора векторного поля.

%

% При вычислениях предполагается, что в объёме тетраэдра

% векторное и скалярное поля изменяются в пространстве по линейному закону.

function [grad,div,rot]=grad_div_rot(nodes,scalar,vector);

a=inv([ones(4,1) nodes]); % Матрица коэффициентов линейной интерполяции

grad=(a(2:end,:)*scalar).'; % Компоненты градиента скалярного поля

div=[a(2,:) a(3,:) a(4,:)]*vector(:); % Дивергенция векторного поля

rot=sum(cross(a(2:end,:),vector.'),2).';

Пример запуска разработанной m-функции:

>> nodes=10*rand(4,3)

nodes =3.5287 2.0277 1.9881 8.1317 1.9872 0.15274 0.098613 6.0379 7.4679 1.3889 2.7219 4.451

>> scalar=rand(4,1)

scalar = 0.93181 0.46599 0.41865 0.84622

>> vector=rand(4,3)

vector = 0.52515 0.01964 0.50281 0.20265 0.68128 0.70947 0.67214 0.37948 0.42889

0.83812 0.8318 0.30462

>> [grad,div,rot]=grad_div_rot(nodes,scalar,vector)

grad = -0.16983 -0.03922 -0.17125

div = -1.0112

rot = -0.91808 0.20057 0.78844

Если предположить, что пространственные координаты измеряются в метрах, а векторное и скалярное поля - безразмерные, то в данном примере получилось:

grad Ф = (-0.16983* 1 _x - 0.03922* 1 _y - 0.17125* 1 _z) м^-1;

div F = -1.0112 м^-1;

rot F = (-0.91808* 1 _x + 0.20057* 1 _y + 0.78844* 1 _z) м^-1.

Дата добавления: 2014-01-04