Несинусоидальные ЭДС, напряжения и токи

НЕСИНУСОИДАЛЬНЫЕ ТОКИ

ЛЕКЦИЯ №24

До сих пор рассматривались линейные цепи при действии постоянных или синусоидальных источников. На практике ЭДС, напряжения и токи в той или иной степени отличаются от постоянных или синусоидальных, причем зависимость от времени может быть периодической, почти периодической и непериодической.

В машинных генераторах искажения формы кривой возникают из-за несинусоидального распределения магнитной индукции вдоль воздушного зазора. В цепях с нелинейными элементами (электрическая дуга, катушка со стальным сердечником, вентили) даже при синусоидальных ЭДС возникают несинусоидальные напряжения и токи. В различных областях радиотехники, автоматики и т.д. применяются статические генераторы, вырабатывающие импульсы пилообразной, ступенчатой и прямоугольной формы. Все перечисленные сигналы относятся к периодическим токам.

Если сложить несколько синусоидальных сигналов разной частоты, то получим непериодический сигнал, который имеет периодическую огибающую, и свойства такого сигнала близки к свойствам периодических сигналов. Поэтому подобные сигналы называются почти периодическими.

При передаче последовательности импульсов или в случае помех и шумов приходится иметь дело с непериодическими сигналами.

Во всех задачах со сложными несинусоидальными кривыми необходимо свести сложную задачу к более простой и применить методы расчета простых цепей.

Всякая периодическая функция f (w t), удовлетворяющая условиям Дирихле, т.е. имеющая на всяком конечном интервале конечное число разрывов первого рода и конечное число максимумов и минимумов, может быть разложена в тригонометрический ряд:

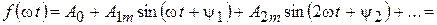
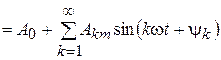. (8.1)

Первый член ряда A ₀ называется постоянной составляющей или нулевой гармоникой, второй член A _{1 m} sin(w t + y₁) – основной или первой гармоникой, а остальные члены вида A_km sin(k w t + y _k) при k > 1 носят название высших гармоник; w = 2p/ T – основная угловая частота; T – период несинусоидальной периодической функции.

После раскрытия синуса суммы это выражение запишется как

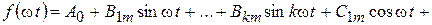
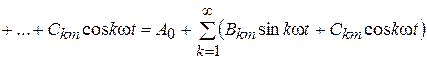. (8.2)

Здесь B_km = A_km cos y _k; C_km = A_km sin y _k.

Коэффициенты A ₀, B_km, C_km могут быть вычислены при помощи следующих интегралов:

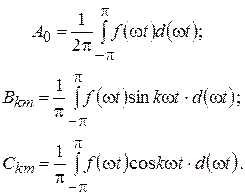(8.3)

Постоянная составляющая равна среднему значению функции за период.

Введя условно отрицательные частоты, исходную функцию можно записать в более компактном виде:

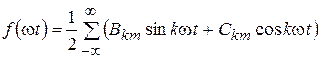. (8.4)

Постоянная составляющая в этом выражении получается при k = 0.

Если воспользоваться формулой Эйлера

,

,

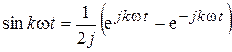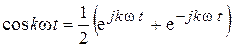то получим

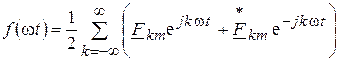, (8.5)

где .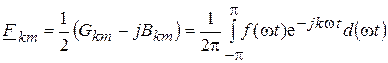

С учетом того, что F_{– km} = F _km, a 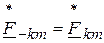, это выражение можно упростить:

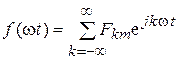. (6.6)

Комплексная форма записи ряда Фурье имеет большое значение при частотном анализе свойств электрических цепей.

Значительное число функций, с которыми приходится иметь дело в электротехнике, удовлетворяют условию f (w t) = – f (w t + p). Такие функции называются симметричными относительно оси абсцисс. Они не содержат четных гармоник и постоянной составляющей:

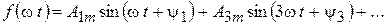(6.7)

В схемах выпрямления приходится иметь дело с функциями, удовлетворяющими условию f (w t) = f (–w t). Такие функции называются симметричными относительно оси ординат. Они не содержат синусных составляющих:

(8.8)

Совокупность гармонических составляющих несинусоидальной периодической функции называется ее дискретным частотным спектром. Спектр можно характеризовать некоторой зависимостью A_km (спектр амплитуд) и y _k (спектр фаз) от частоты k w.

Дата добавления: 2014-01-04