Несинусоидальных периодических ЭДС, напряжений и токов

Максимальные, действующие и средние значения

Периодическая функция f (w t), помимо гармонических составляющих, характеризуется: максимальным значением за период a _max, действующим значением

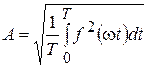
и средним по модулю значением

.

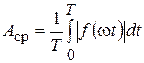Если кривая f (w t) симметрична относительно оси абсцисс и в течение половины периода ни разу не меняет знак, то среднее по модулю значение равно среднему значению за половину периода. Если за весь период функция ни разу не изменяет знак, то среднее по модулю значение равно постоянной составляющей.

В расчетах обычно пользуются действующими значениями. Если кривая периодически изменяющейся функции разложена в тригонометрический ряд, то действующее значение может быть найдено следующим образом:

.

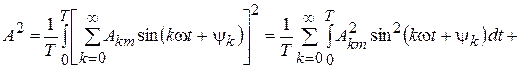
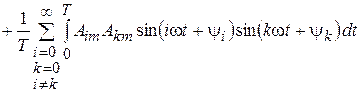Каждый из интегралов в последней сумме равен нулю, поэтому

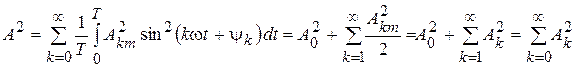. (8.8)

Следовательно,

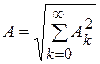. (8.9)

Таким образом, действующее значение периодической несинусоидальной функции зависит только от действующих значений ее гармоник и не зависит от их начальных фаз y _k.

Если известны действующие значения гармонических составляющих какой-то несинусоидальной функции, то действующее значение найдем по формуле

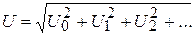. (8.10)

При оценке несинусоидальных функций в электроэнергетике пользуются коэффициентом формы кривой k _ф, коэффициентом амплитуды k _а, коэффи­циентом искажения k _и.

Коэффициент формы определяется как отношение действующего значения к среднему по модулю значению:

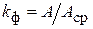. (8.11)

Для синусоиды .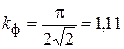

Коэффициент амплитуды равен отношению максимального значения к действующему значению

k _а = a _max/A. (8.12)

Для синусоиды .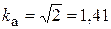

Коэффициент искажения определяется как отношение действующего значения основной гармоники к действующему значению всей кривой

k _и = A ₁/ A. (8.13)

Для синусоиды k _и = 1.

В электронике для оценки искажений пользуются коэффициентом гармоник, который равен отношению действующего значения высших гармоник к действующему значению основной гармоники

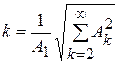. (8.14)

Для синусоиды k = 0.

Дата добавления: 2014-01-04