Несинусоидальные кривые с периодической огибающей

Это кривые, относящиеся к классу почти периодических. Они также разлагаются на гармонические составляющие. Период таких кривых обычно во много раз превышает период любой из составляющих и может стремиться к бесконечности. К числу явлений, характеризуемых такими кривыми, относятся биения и модуляции.

Биения. Простейший случай получается при сложении двух синусоид с равными амплитудами, но не равными частотами w₁ и w₂, причем w₁ > w₂:

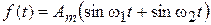. (8.15)

Преобразуя сумму синусов, получим

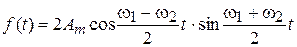. (8.16)

Можно считать, что кривая f (t) представляет собой синусоиду с угловой частотой 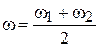, амплитуда которой изменяется по косинусоиде со значительно меньшей угловой частотой 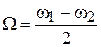, тогда

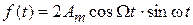. (8.17)

Частотой биений называется частота 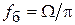, равная числу максимумов огибающей кривой в единицу времени.

Пример несинусоидальной кривой с периодической огибающей показан на рис. 8.1.

Период биений 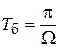в общем случае не равен периоду кривой f (t).

Модулированные колебания. Синусоидально изменяющаяся величина f (t) = = A_m sin(w t + y) задается тремя параметрами: амплитудой A_m, угловой частотой w и начальной фазой y. Эти величины не зависят от времени. Однако для передачи различного рода сигналов применяются генераторы, в которых одна из этих величин изменяется по некоторому заданному закону. Изменение во времени одного из параметров A_m, w или y называют модуляцией. Различают амплитудную, частотную и фазовую модуляции.

Пусть функция, изменяющаяся с частотой w₀ и амплитудой A_m (t), модулирована гармоническим сигналом с частотой W < w₀ относительно среднего значения A _{0 m} , т.е. с законом изменения A_m (t) (рис.8.2):

. (8.18)

Частота w₀ называется несущей частотой, частота W – модулирующей частотой, m – коэффициентом модуляции.

При определении токов или напряжений модулированные по амплитуде колебания могут быть разложены на синусоидальные составляющие

.

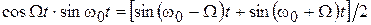Тогда

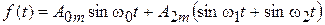, (8.19)

где ; .

		Рис. 8.2. Модулированная функция f (t)

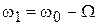Таким образом, простейшие модулированные по амплитуде колебания могут быть представлены в виде суммы трех синусоидальных колебаний с несущей частотой w₀, боковыми частотами w₁, w₂ и постоянными амплитудами.

Под действующим значением колебаний с периодической огибающей, описываемых функцией 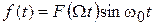, обычно понимают действующее значение огибающей, деленное на :

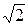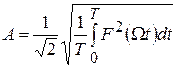, (8.20)

где T = 2p/W.

Этим выражением можно пользоваться, если исследуется неперио­дический процесс за достаточно больной промежуток времени.

Дата добавления: 2014-01-04