Расчет переходных процессов операторным методом

Рассмотрим сначала несколько простых примеров, исследованных ранее классическим методом.

1. При включении RL -цепи под постоянное напряжение u = U = const имеем

U (p) = U / p; Z (p) = pL + R.

При нулевом начальном условии i (0) = 0

.

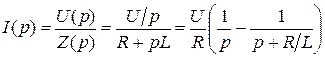Искомый ток

.

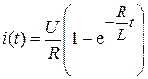2. При включении RC -цепи под постоянное напряжение при u_C (0) = 0 имеем

,

.

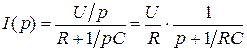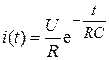3. При включении RLC -цепи под постоянное напряжение при нулевых начальных условиях

,

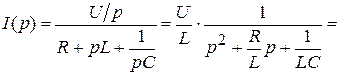
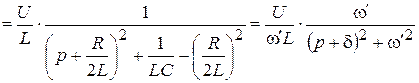где .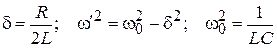

Оригинал этого изображения

.

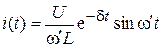4. Главное достоинство операторного метода для расчета переходных процессов, заключающееся в алгебраизации дифференциальных уравнений цепи, особенно проявляется при расчете сложных цепей. Ранее было доказано, что, учитывая члены L_ki_k (0) и u_Ck (0)/ p как добавочные ЭДС, можно применить к расчету переходных процессов все методы расчета сложных цепей.

Рассмотрим переходный процесс в следующей цепи (рис. 10.2):

По методу контурных токов

,

		Рис. 10.2. Схема цепи

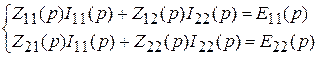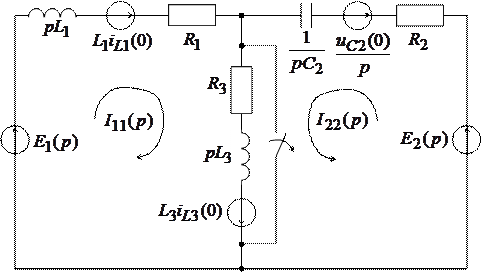где

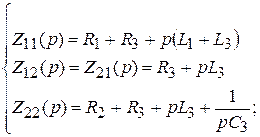
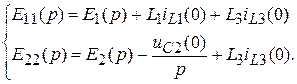
Решение уравнений

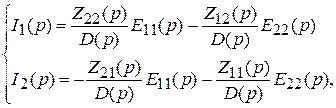
где D (p) = Z ₁₁(p) Z ₂₂(p) – Z ²₁₂(p).

Пусть е ₁ = Е ₀ = const; e ₂ = E_m sin w t.

Изображения этих функций

.

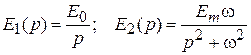Если подставить эти изображения ЭДС в формулу для токов, то видно, что последнее представляет собой рациональную дробь, где числитель и знаменатель являются полиномами оператора p. Как правило, в таблицах формулы соответствия оригиналов и изображений приведены только для полиномов относительно низкого порядка.

Дата добавления: 2014-01-04