Поле двух параллельных заряженных осей

Пусть одна ось имеет линейный заряд + t, а другая – - t. Возьмем в поле некоторую произвольную точку М (рис. 15.8).

Результирующая напряженность поля в точке М 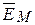равна геометрической сумме напряженностей от обоих зарядов. Потенциал – функция скалярная, и он равен сумме потенциалов от каждой оси

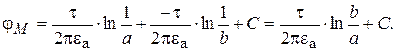(15.28)

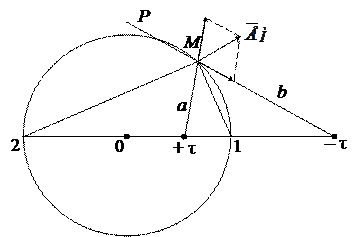Уравнением эквипотенциали в поле двух заряженных осей является выражение b/a = const, т.е. эквипотенциаль представляет собой совокупность точек, отношение расстояний которых до двух заданных точек есть величина постоянная. Из геометрии известно, что такой совокупностью точек является окружность. Для ее построения соединим точку М с осями. Проведем биссектрису внутреннего (aMb) и внешнего (pMa) углов. Точки 1 и 2 пересечения биссектрис с линией, проведенной через заряженные оси, и точка М будут тремя точками окружности. Для нахождения положения центра окружности (точки О) разделим пополам расстояние между точками 1 и 2.

Рис. 15.8. Поле двух заряженных осей

Рассмотрим поле двухпроводной линии (рис. 15.9).

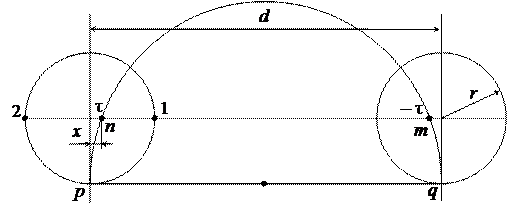Рис. 15.9. К рассмотрению поля двухпроводной линии

Заряды проводов по поверхности распределены с неодинаковой плотностью.

Задача о поле двухпроводной линии может быть сведена к задаче о поле двух заряженных осей.

Пусть заряженные оси будут расположены в точках m и n. Из условия симметрии они удалены на одинаковое расстояние x от геометрических осей проводов О ₂ и О ₁.

Для точки 1 отношение b/a будет 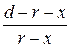, для точки 2 – .

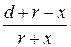Из равенства 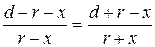получим

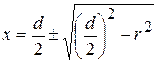. (15.29)

Знак минус перед радикалом соответствует положению точки n, знак плюс – точке m.

Точки m и n называют электрическими осями проводов. Их можно получить геометрическим построением. Проводится линия, параллельная линии, соединяющей оси проводов и касательная к поверхности проводов. Через точки касания поводится окружность диаметром d. Пересечение этой окружности с линией соединяющей оси проводов даст положение электрических осей.

Определим емкость двухпроводной линии

;

;

;

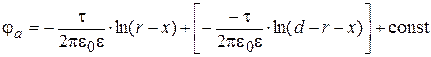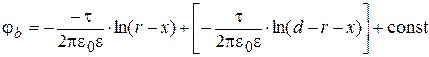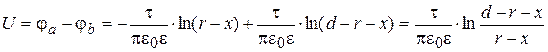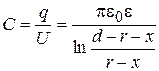. (15.30)

Дата добавления: 2014-01-04