Коефіцієнт чутливості бета

Аспірантом Марковича, який у подальшому розділив з ним нобелівську премію, Вільямом Шарпом була розроблена широко відома модель оцінки довгострокових фінансових активів (Capital Asset Pricing Model, САРМ), що дозволяє проводити оцінку цінних паперів для випадків, коли всі ін­вестори формують свої портфелі у відповідності з реко­мендаціями Марковича. Ця модель створена для опису середнього відхилення курсів окремих акцій або інших цінних паперів відносно ринку в цілому за певний період використовує показник систематичного ризику, або коефіцієнт чутливості бета (b).

8.4.1. Спрощена класична модель формування портфеля (модель Шарпа)

Найпростішою і широко використовуваною на практиці математичною моделлю для наближених розрахунків є запропонована Вільямом Шарпом однофакторна модель.

Ця модель ґрунтується на багаторічних спостереженнях і виявленні того факту, що норми прибутків більшості акцій, в основному, залежать від одного чинника, який називають чинником ринку (біржі). На більшості бірж спостерігається, що із зростанням ринкових індексів зростають пропорційно і ціни більшості акцій, і навпаки. Ці спостереження дозволили висунути гіпотезу, згідно з якою норми прибутку акцій щільно корельовані відносно загальнобіржового індексу доходів (середньому по біржі в цілому).

Цей індекс можна трактувати як гіпотетичний цінний папір (акцію), ціна якого весь час коливається і для якого, зокрема, можна визначити сподівану норму прибутку і варіацію. Цей гіпотетичний ЦП можна прийняти за портфель ринку.

Кореляційну залежність норми прибутку звичайної акції від норми прибутку, що її вказує ринковий індекс, можна подати за допомогою лінійної економетричної моделі (моделі Шарпа):

R_j = a _j + b _j R_М + e_j.

У моделі Шарпа величина R_j – норма прибутку j -ої акції – пояснюється нормою прибутку ринкового портфеля – R_М. Але оскільки на норму прибутку акції впливає також ряд інших чинників, крім загальної ситуації на біржі (що відображає R_М), то дію інших (неврахованих) чинників відображає випадкова складова е_j. Власне, введення цієї випадкової величини дозволяє поставити знак рівності між лівою і правою частинами розглянутої моделі.

Коефіцієнт b _j при величині R_М в моделі Шарпа називають коефіцієнтом бета для j -ої акції. Він відіграє дуже важливу роль в економічній науці та практиці і може використовуватись як міра ринкового ризику певної акції.

Йому можна дати таку інтерпретацію: коефіцієнт b звичайної акції вказує, на скільки відсотків наближено зросте (знизиться) норма прибутку акції, якщо норма прибутку ринку зросте (знизиться) на 1%. Тобто це означає, що коефіцієнт b певної акції показує, якою мірою норма прибутку акції реагує на зміни, що відбуваються на ринку в цілому.

Наведемо кілька простих прикладів.

1. Коефіцієнт b дорівнює нулеві (b _j = 0). Це означає, що норма прибутку даного цінного паперу ніяк не реагує на зміни на ринку. Тобто даний цінний папір необтяжений ринковим ризиком. Таким папером може бути, зокрема, державна облігація, для якої норма прибутку майже позбавлена ризику.

2. Величина коефіцієнта b така, що 0 < b _j < 1. Це означає, що норма прибутку даної акції досить помірковано реагує на зміни, які відбуваються на ринку цінних паперів. Таку акцію називають дефенсивною (захищеною) акцією.

3. Коефіцієнт b дорівнює одиниці (b _j = 1). Це означає, що норма прибутку даної акції змінюється такою самою мірою, як і норма прибутку ринку. Слід мати на увазі, що ринковий портфель має коефіцієнт b = 1.

4. Величина коефіцієнта b більша від одиниці (b _j > 1). Це означає, що норма прибутку даної акції значною мірою залежить від змін, що відбуваються на ринку. Таку акцію називають агресивною.

В Україні останнім часом в періодичних виданнях почали публікуватися дані щодо цього, але досить нерегулярно. В країнах з розвинутою ринковою економікою ряд солідних часописів систематично публікують коефіцієнт b для багатьох акцій. Більшість акцій Нью-Йоркської біржі мають коефіцієнт b, який знаходиться в інтервалі від 0,5 до 1,5.

Викладені вище засади класичної моделі мають широке застосування. У фірмах під час прийняття рішень коефіцієнти b використовують для обчислення ціни необхідного капіталу для інвестиційних проектів.

Якщо частки акцій в ПЦП становлять відповідно х_j, j = 1, ..., n, а також відомі коефіцієнти b _j, j = 1, ..., n, то можна показати, що коефіцієнт b портфеля (b _П) обчислюється за формулою:

.

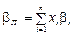Приклад 8.3. Нехай інвестор сформував портфель, 40% якого становлять державні (майже безризикові) акції, 25% капіталу він вклав у акції виду А ₁, для яких коефіцієнт b₁ = 0,5, решту 35% вклав у акції виду А ₂, для яких b₂ = 1,2. Необхідно обчислити коефіцієнт b портфеля.

Розв’язання. Використовуючи формулу (7.27), одержимо:

b _П = 0,4 × 0 + 0,25 × 0,5 + 0,35 × 1,2 = 0,545.

Отже, портфель інвестора характеризується низьким ступенем ризику ринку. Це досягнуто за рахунок того, що в структурі портфеля велику частку мають державні акції.

Дата добавления: 2014-01-04