Разложения

Определение оригинала по изображению. Теорема

Операторным методом

Алгоритм анализа переходных процессов

Расчет переходного процесса операторным методом предусматривает следующий порядок операций:

1) вычерчивается исходная расчетная схема замещения цепи и определяются начальные условия коммутации;

2) все известные электрические величины и параметры изображаются в операторной форме (сложение функции – с помощью таблиц оригиналов и изображений) и осуществляется переход к операторной схеме замещения цепи;

3) на основе законов Ома, Кирхгофа в операторной форме в соответствии с выбранным методом расчета цепи после ее коммутации составляется система операторных уравнений с учетом начальных условий, которая решается относительно изображений искомых переходных токов и напряжений;

4) получение изображения искомых переходных токов и напряжений преобразуются либо к табличным, либо к виду, удобному для применения теоремы разложения, и определяются оригиналы (переходные токи и напряжения);

5) производится анализ характера переходного процесса.

При использовании операционного исчисления расчеты ведут в изображениях функций, что обеспечивает алгебраизацию задачи, а затем на заключительном этапе переходят к оригиналам (функциям времени).

Наиболее распространенными являются следующие способы перехода к оригиналам:

- с помощью таблиц оригиналов и изображений;

- с помощью обратного преобразования Лапласа;

- на основе теоремы разложения.

Определение оригиналов по таблицам возможно тогда, когда удается свести изображение функции к табличному. В сложных случаях этого достичь не удается.

Определение оригиналов с помощью обратного преобразования Лапласа (13.3) производится в наиболее сложных случаях, приводит к громоздким вычислениям и требует специальной подготовки.

Определение оригиналов на основе теоремы разложения является наиболее универсальным способом и используется в тех случаях, когда полученное изображение функции не удается свести к табличному.

Теорема разложения формулируется следующим образом.

Если изображение искомой функции можно представить в виде рациональной дроби

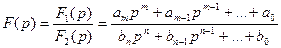(14.14)

Где многочлены F₁(p) и F₂(p) общих корней не имеют;

a_k и b_k – действительные числа, то F(p) можно разложить на ряд слагаемых, каждому из которых соответствует табличный интеграл

(14.15)

где p₁,p₂,...,p_n – корни характеристического уравнения F₂(p) = 0;

F₁(p₁),F₁(p₂),…,F₁(p_n) – значения многочлена числителя при соответствующих корнях

p₁,p₂,…,p_n характеристического уравнения;

- значения производных многочлена знаменателя при соответствующих корнях p₁,p₂,…,p_n характеристического уравнения.

Алгоритм применения теоремы разложения.

1. Изображение искомой функции представить в виде рациональной дроби (14.14).

2. Составить характеристическое уравнение знаменателя и определить его корни p₁,p₂,…,p_n.

3. Определить значения многочлена числителя при каждом из корней характеристического уравнения.

4. Определить в общем виде производную многочлена знаменателя и ее значения при каждом из корней характеристического уравнения.

5. По теореме разложения (14.15) записать оригинал (искомую функцию).

Пример. Пусть задано изображение в виде .

Необходимо найти его оригинал.

Решение.

Обозначим F₁(p) = p +2; F₂(p) = p(p² + 5p +4).

При этом получим F(p) в виде (14.14).

Найдем корни характеристического уравнения F₂(p) = p(p² + 5p +4) = 0.

p₁ = 0; p₂ = - 1; p₃ = - 4.

При этом F₁(p₁) = 2; F₁(p₂) = 1; F₁(p₃) = - 2.

Определим производную

Отсюда

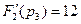
Воспользовавшись формулой (12.9), окончательно получим:

Дата добавления: 2014-01-04