МЕДИАННая ФИЛЬТРАЦИя комбинированных помех

Комбинированные помехи. При регистрации, обработке и обмене данными в современных измерительно-вычислительных и информационных системах потоки сигналов кроме полезного сигнала s(t-t₀) и флуктуационных шумов q(t) содержат, как правило, импульсные потоки g(t)=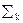d(t-t_k) различной интенсивности с регулярной или хаотической структурой

x(t) = s(t-t₀) + g(t) + q(t). (16.2.1)

Причиной появления импульсных потоков могут быть как внешние импульсные электромагнитные помехи, так и наводки, сбои и помехи в работе самих систем. Совокупность статистически распределенного шума и потока квазидетерминированных импульсов представляет собой комбинированную помеху. Радикальный метод борьбы с комбинированной помехой - применение помехоустойчивых кодов. Однако это приводит к снижению скорости и усложнению систем приемо-передачи данных. Простым, но достаточно эффективным альтернативным методом очистки сигналов в таких условиях является двухэтапный алгоритм обработки сигналов x(t), где на первом этапе производится устранение из потока x(t) шумовых импульсов, а на втором – очистка сигнала частотными фильтрами от статистических шумов. Для сигналов, искаженных действием импульсных шумов, отсутствует строгая в математическом смысле постановка и решение задачи фильтрации. Известны лишь эвристические алгоритмы, наиболее приемлемым из которых является алгоритм медианной фильтрации.

Очистка сигналов от квазидетерминированного шума. Допустим, что шум q(t) представляет собой статистический процесс с нулевым математическим ожиданием, полезный сигнал s(t-t₀) имеет неизвестное временное положение t₀ Î [0, T], а поток шумовых импульсов g(t) имеет вид:

g(t) =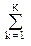e_k a_k g(t-t_k), (16.2.2)

где a_k - амплитуда импульсов в потоке, t_k - неизвестное временное положение импульсов, e_k=1 с вероятностью p_k и e_k=0 с вероятностью 1-p_k. Такое задание импульсной помехи соответствует потоку Бернулли /44/.

При применении к потоку x(t) скользящей медианной фильтрации с окном N отсчетов (N – нечетное) медианный фильтр подавляет импульсные помехи, если количество импульсов в пределах апертуры не превосходит (N-1)/2. В этом случае, при p_k = p для всех импульсов помехи, вероятность подавления помех может быть определена по выражению /3i/:

R(p) =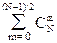p^m(1-p)^N-p. (16.2.3)

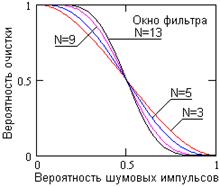Рис. 16.2.1.

На рис. 16.2.1 приведены результаты расчетов вероятности подавления импульсной помехи медианным фильтром.

При p<0.5 результаты статистического моделирования процесса показывают хорошее соответствие расчетным значениям. Для интенсивных импульсных шумовых потоков при p>0.5 медианная фильтрация становится мало эффективной, т.к. происходит не подавление, а усиление и трансформация его в поток импульсов другой структуры (со случайной длительностью).

Преобразование статистики шумов. Медианная фильтрация является нелинейной операцией над входным процессом, которая наряду с исключением импульсных помех изменяет и распределение статистических шумов q(t), что может быть нежелательным для построения последующих фильтров. Аналитический расчет преобразования статистики шумов затруднителен из-за слабой разработанности соответствующего математического аппарата.

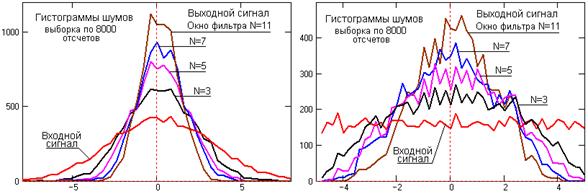Рис. 16.2.2. Гистограммы шумовых сигналов.

На рис. 16.2.2 приведены примеры медианной фильтрации модельных шумовых сигналов с гауссовым и равномерным распределением при различной ширине окна фильтра. Как следует из этих графиков, при фильтрации происходит преимущественное подавление шумовых сигналов с большими отклонениями отсчетов от среднего значения с уменьшением стандарта (СКО - среднеквадратического отклонения) распределения. Уменьшение стандарта тем больше, чем больше окно фильтра. Этим же определяется и преобразование формы распределения выходного равномерного шума (а равно и других распределений шумов) к гауссовой по мере увеличения размера окна фильтра.

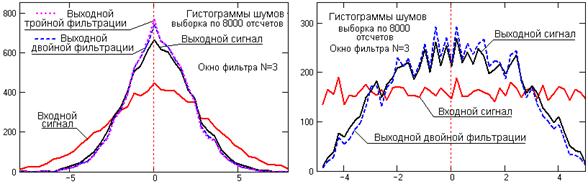Рис. 16.2.3.

На рис. 16.2.3 приведен пример изменения гистограмм шума при выполнении дву- и трехкратной последовательной фильтрации. Как видно из графиков, основной эффект фильтрации достигается на первом цикле.

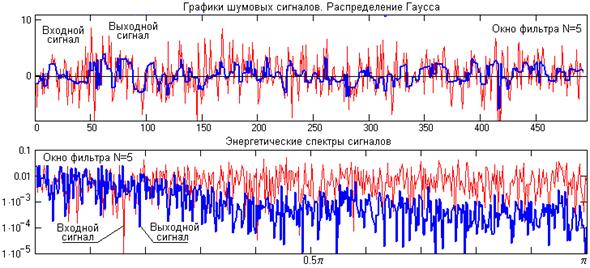Рис. 16.2.4.

Уменьшение количества больших шумовых отклонений от среднего значения шума приводит также к изменению спектра шума и к определенному подавлению его высокочастотных составляющих, которых больше в "хвостах" шумовых распределений. Это можно видеть на рис. 16.2.4 на спектрах плотности мощности входного и выходного сигналов. Следует, однако, заметить, что нелинейность медианной фильтрации (замена больших отклонений средними по рангу в окне) приводит к повышению низкочастотных составляющих спектра шума. Этот эффект наглядно виден на рис. 12.2.5, где приводятся сглаженные значения отношения модулей спектров выходного модельного шумового сигнала к входному, т.е. эквивалент коэффициента передачи фильтром шумовых сигналов. На коэффициент передачи фильтром полезных низкочастотных сигналов это не отражается, он остается равным 1, но может приводить к ухудшению отношения сигнал/шум.

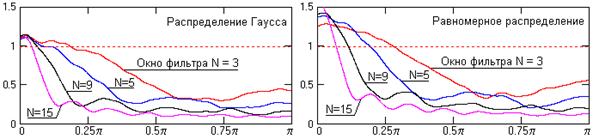Рис. 16.2.5.

Попутно заметим, что медианный фильтр можно применять и по прямо противоположному назначению – обнаружению в сигналах и выделению квазидетерминированных помех.

литература

Большаков И.А., Ракошиц В.С. Прикладная теория случайных потоков, М.: Сов. радио, 1978,- 248с.

Яровой Н.И. Адаптивная медианная фильтрация.

Черненко С.А. Медианный фильтр.

Радченко Ю.С. Эффективность приема сигналов на фоне комбинированной помехи с дополнительной обработкой в медианном фильтре. – "Журнал радиоэлектроники", №7, 2001.

ЛИТЕРАТУРА

1. Антонью А. Цифровые фильтры: анализ и проектирование. – М.: Радио и связь, 1983. – 320 с.

2. Баскаков С.И. Радиотехнические цепи и сигналы: Учебник для вузов. - М.: Высшая школа, 1988.- 448 с.

3. Бат М. Спектральный анализ в геофизике. - М.: Недра, 1980.- 535 с.

4. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. – М.: Мир, 1989. – 540 с.

5. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов. – М.: Мир, 1989. – 448 с.

6. Вычислительная математика и техника в разведочной геофизике: Справочник геофизика. – М.: Недра, 1990. – 498 с.

7. Гольденберг Л.М. и др. Цифровая обработка сигналов: Справочник. - М.: Радио и связь, 1985.- 312 с.

8. Гольденберг Л.М. и др. Цифровая обработка сигналов: Учебное пособие для вузов. - М.: Радио и связь, 1990.- 256 с.

9. Гутников В.С. Фильтрация измерительных сигналов. – Л.: Энергоатомиздат, 1990. – 192 с.

10. Даджион Д., Мерсеро Р. Цифровая обработка многомерных сигналов. – М.: Мир, 1988. – 488 с.

11. Дмитриев В.И. Прикладная теория информации: Учебник для студентов вузов. - М.: Высшая школа, 1989.- 325 с.

12. Канасевич Э.Р. Анализ временных последовательностей в геофизике. - М.: Недра, 1985.- 300 с.

13. Клаербоут Д.Ф. Теоретические основы обработки геофизической информации с приложением к разведке нефти. – М.: Недра, 1981. – 304 с.

14. Кулханек О. Введение в цифровую фильтрацию в геофизике. – М.: Недра, 1981. – 198 с.

15. Купер Дж., Макгиллем А. Вероятностные методы анализа сигналов и систем. – М.: Мир, 1989. – 376 с.

16. Макс Ж. Методы и техника обработки сигналов при физических измерениях: В 2-х томах. - М.: Мир, 1983.

17. Марпл-мл. С.Л. Цифровой спектральный анализ и его приложения. – М.: Мир, 1990. – 584 с.

18. Никитин А.А. Теоретические основы обработки геофизической информации: Учебник для вузов. - М.: Недра, 1986.- 342 с.

19. Оппенгейм А.В., Шафер Р.В. Цифровая обработка сигналов. – М.: Связь, 1979. – 416 с.

20. Отнес Р., Эноксон Л. Прикладной анализ временных рядов. – М.: Мир, 1982. – 428 с.

21. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. – М.: Мир, 1978. – 848 с.

22. Рапопорт М.Б. Вычислительная техника в полевой геофизике: Учебник для вузов. - М.: Недра, 1993.- 350 с.

23. Сиберт У.М. Цепи, сигналы, системы. – М.: Мир, 1988. – 336 с.

24. Хемминг Р.В. Цифровые фильтры. – М.: Недра, 1987. – 221 с.

25. Лосев А.К. Линейные радиотехнические цепи: Учебник для вузов. - М.: Высшая школа, 1971. - 560 с.

26. Васильев Д.В. Радиотехнические цепи и сигналы: Учебное пособие для вузов. - М.: Радио и связь, 1982. - 528 с.

27. Зиновьев А.Л., Филиппов Л.И. Введение в теорию сигналов и цепей: Учебное пособие для вузов. - М.: Высшая школа, 1975. - 264 с.

28. Севостьянов Б.А. Курс теории вероятностей и математической статистики. - М.: Наука, 1982. - 256 с.

29. Коваленко И.Н., Филиппова А.А. Теория вероятностей и математическая статистика: Учебное пособие. - М.: Высшая школа, 1982. - 256 с.

30. Худсон Д., Статистика для физиков. - М.: Мир, 1970. - 296 с.

31. Гурский Е.И. Теория вероятностей с элементами математической статистики: Учебное пособие для вузов. - М.: Высшая школа, 1971.- 328 с.

32. Вероятностные методы в вычислительной технике: Учеб. пособие для вузов / А.В.Крайников и др. - М.: Высшая школа, 1986. - 312 с.

33. Игнатов В.А. Теория информации и передачи сигналов. - М.: Советское радио, 1979.

34. Дьяконов В., Абраменкова И. MATLAB. Обработка сигналов и изображений. Специальный справочник. – СПб.: Питер, 2002, 608 с.

35. Астафьева Н.М. Вейвлет-анализ: Основы теории и примеры применения. / Успехи физических наук, 1996, т.166, № 11, стр. 1145-1170.

36. Дремин И.Л. и др. Вейвлеты и их использование. / Успехи физических наук, 2001, т.171, № 5, стр. 465-501.

37. Петухов А.П. Введение в теорию базисов всплесков. – СПб.: Изд. СПбГТУ, 1999, 132 с.

38. Адаптивные фильтры. /Под ред. К.Ф.Н.Коуэна и П.М.Гранта. – М.: Мир, 1988, 392 с.

39. Дьяконов В.П. Вейвлеты. От теории к практике. – М.: СОЛОН-Р, 2002. – 448 с.

40. Корн Г., Корн Е. Справочник по математике для научных работников и инженеров. – М.: Наука, 1984.

41. Овечкина Е.В. (НТИ УГТУ-УПИ), Поршнев С.В. (УГТУ-УПИ). Разработка методов оптимальной аппроксимации эмпирических зависимостей. (Статья в электронном журнале).

42. Новиков Л.В. Основы вейвлет-анализа сигналов. Учебное пособие. СПб, ИАнП РАН, 1999

43. Айфичер Э., Джервис Б. Цифровая обработка сигналов. Практический подход. / М., "Вильямс", 2004, 992 с.

Дата добавления: 2014-01-04