Различные уравнения прямой в пространстве

И плоскости в пространстве

Прямая в пространстве. Различные задачи на прямые

Лекция 13

Положение прямой в пространстве определяется полностью, если даны:

а) две ее точки;

б) точка и направляющий вектор;

в) две плоскости, пересекающиеся по этой прямой.

Пусть в пространстве выбрана аффинная система координат .

1. Каноническое уравнение прямой.

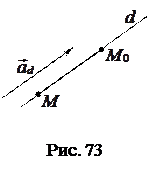Пусть прямая 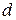задана в пространстве точкой 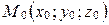и направляющим вектором (рис. 73).

.

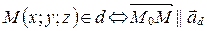Далее применяем условие коллинеарности двух векторов в пространстве в координатах (см. § 5). При этом возможны различные случаи:

а) и . Тогда получаем следующее уравнение прямой:

. (28)

б) .

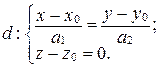(29)

в) (запишите уравнение прямой 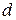самостоятельно).

г) 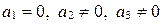(запишите уравнение прямой 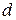самостоятельно).

д) 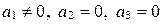. Получаем следующее уравнение прямой :

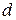(30)

е) (запишите уравнение прямой 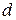самостоятельно).

ж) 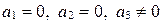(запишите уравнение прямой 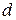самостоятельно).

Уравнения (28)-(30) (а также уравнения, записанные вами в пунктах в), г), е) и ж)) называются каноническими уравнениями прямой в пространстве.

2. Уравнение прямой, заданной двумя точками.

Пусть . Тогда прямую 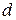можно задать точкой 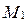и направляющим вектором . Поэтому применяем каноническое уравнение прямой:

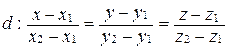. (31)

Уравнение (31) называется уравнением прямой в пространстве, заданной двумя точками.

Если одна или две координаты вектора 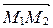окажутся нулевыми, то применяем частные случаи канонического уравнения прямой, т.е. уравнения вида (29) или (30).

3. Параметрическое уравнение прямой.

В случае, когда прямая 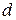задана так же, как в пункте 1 (точкой 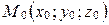и направляющим вектором ), можно получить параметрическое уравнение прямой. 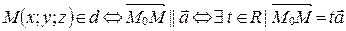(по теореме о коллинеарных векторах). Переходя к координатам, получаем:

откуда

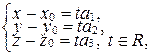
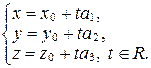(32)

Система уравнений (32) называется параметрическим уравнением прямой в пространстве.

Действительное число 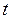в системе (32) называется параметром и имеет такой же смысл, как и параметр 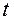в параметрическом уравнении прямой на плоскости (см. § 15).

4. Уравнение прямой, заданной двумя пересекающимися плоскостями.

Пусть 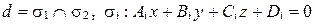в 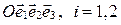(рис. 74).

Точка 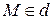тогда и только тогда, когда ее координаты 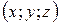являются решением системы уравнений плоскостей и .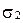

Система уравнений

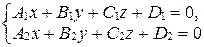(33)

называется уравнением прямой, заданной двумя пересекающимися плоскостями.

Лемма 1. Вектор

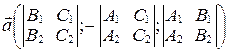(34)

является направляющим вектором прямой .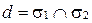

□ Воспользуемся дважды леммой о параллельности вектора и плоскости.

1) Докажем, что .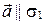

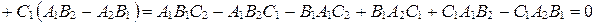. Тогда по лемме о параллельности вектора и плоскости .

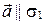2) Докажите самостоятельно, что .

Из пунктов 1) и 2) следует, что 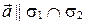, т.е. . ■

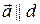Итак, из леммы 1 следует, что если прямая 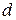задана как линия пересечения двух плоскостей 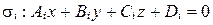, , то координаты ее направляющего вектора находятся по формуле (34).

Замечание. Как и в случае прямой на плоскости, переменные 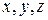в уравнениях (28)-(33) называются текущими координатами точек прямой в пространстве.

Задания для самостоятельной работы

1. Можно ли пользоваться уравнениями (28)-(30) в прямоугольной декартовой системе координат 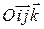в пространстве и почему?

2. Найдите тремя способами уравнение каждой из осе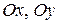й и 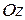аффинной системы координат (каноническое, параметрическое уравнения и уравнение оси как линии пересечения координатных плоскостей).

3. Дано каноническое уравнение прямой . Приведите его к виду (33).

4. Дано параметрическое уравнение (32) прямой 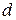. Приведите его к виду (33).

5. Дано уравнение (33) прямой 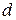. Получите из него каноническое и параметрическое уравнения прямой .

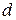6. Докажите, что уравнение плоскости, проходящей через точку 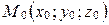параллельно прямым 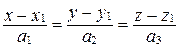и может быть представлено в следующем виде:

.

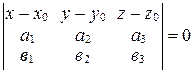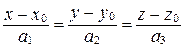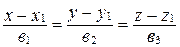7. Докажите, что если две прямые и пересекаются, то уравнение плоскости, в которой они лежат, может быть представлено в следующем виде:

.

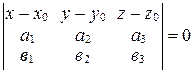8. Докажите, что уравнение плоскости, проходящей через прямую 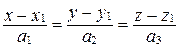параллельно прямой 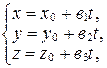может быть представлено в следующем виде:

.

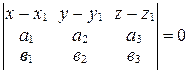Дата добавления: 2014-01-04