Окно Хемминга

Оптимальное окно.

Различным последовательностям весовых множителей отвечают фильтры с различными свойствами. Естественно, возникает вопрос об отыскании наилучшего набора коэффициентов {ω_k} и отвечающей ему функции W(ω). При этом ясно, что, в силу механизма происхождения пульсаций, бороться с ними можно, изменяя форму окна, в то время как длина фильтра определяет ширину центрального лепестка и, следовательно, увеличивая N, можно добиться уменьшения "размыва" частотной характеристики G(ω).

Анализ равенства (10) и графиков на рис.2 позволяет сделать следующие выводы относительно оптимального окна. Коэффициенты {ω_k} должны быть такими, чтобы

- во-первых, функция W(ω) имела бы как можно более узкий главный лепесток (тогда эффект размывания максимально ослабиться);

- во-вторых, боковые лепестки должны иметь по возможности минимальную амплитуду (чтобы пульсации и выбросы были менее заметны).

Существует большое число окон просмотра данных. Ниже будут упомянуты две попытки построения оптимального, в смысле сформулированных требований, окна.

Рассмотрим весовые множители вида

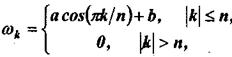(16)

где a, b - варьируемые параметры, потребуем, чтобы a+b=1. Как частные случаи, отметим:

- a=0, b=1 - прямоугольное окно;

- a=0.5, b=0.5 - окно Ганна.

Хеммингом была поставлена задача вычисления таких a и b, чтобы максимальная амплитуда боковых лепестков была минимальной. Решение - оптимальные значения а и b являются функцией от N (длины фильтра). Эти функции могут быть найдены численными методами с помощью вычислительной техники. Соответствующие графики даны на рис.3. Обычно полагают a=0.46, b=0.54.

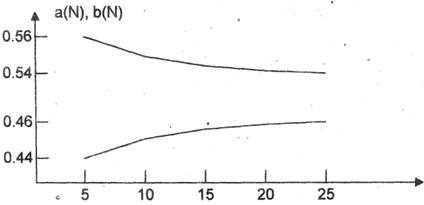
Рис.4.3. Оптимальные значения параметров окна Хемминга.

Дата добавления: 2014-01-04