Сильные и слабые ударные волны в совершенном газе

В п. 4.2 Были выведены соотношения, связывающие параметры на фронте ударной волны для совершенного идеального газа:

(4.40)

Для сильных ударных волн (практически сильными ударными волнами называются волны, для которых P₂/P₁ > 20, давлением P₁ можно пренебречь по сравнению с давлением P_4. В этом случае уравнения, связывающие параметры на фронте сильной ударной волны, принимают простой вид. Если в третьем уравнении системы (4.40), то есть в уравнении ударной адиабаты Гюгонио, в правой части разделить числитель и знаменатель не P₂, то в пределе при P₂ ® ¥ придем к выражению (4.15):

(4.41)

которое показывает, что плотность газа на фронте ударной волны действительно стремится к определенному конечному пределу, зависящему от величины k, то есть в конечном итоге от температуры на фронте ударной волны (см. п. 4.3 - 4.5).

Из первого и второго уравнений системы (4.40) следует выражение

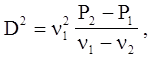(4.42)

которое в случае сильной ударной волны (пренебрегаем P₁ по сравнению с P₂) после дополнительных преобразований будет иметь вид

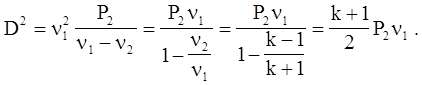
Из этого выражения получаем для давления на фронте сильной ударной волны

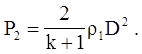(4.43)

Из первого уравнения системы (4.40)

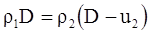
получаем

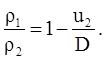
Учитывая соотношение (4.41), получим для массовой скорости в сильной ударной волне

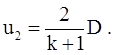(4.44)

Посмотрим теперь, что происходит с ударной волной на большом удалении от места ее возникновения.

В результате интенсивных необратимых энергетических потерь в ударной волне, а также вследствие дивергенции (расхождения) волны ее интенсивность с удалением от места возникновения падает, то есть при r ® ¥ DE ® 0, DP ® 0, D r ® 0.

Скорость ударной волны D, которая больше скорости звука в невозмущенной среде, где распространяется ударная волна, определяется соотношением

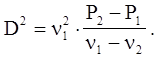
Величина D, когда интенсивность ударной волны сильно падает (P₂» P₁), становится равной скорости звука в невозмущенной среде с₁. Это видно из соотношения для D², если P₂ ® P₁, Dn ® 0:

P₂ ® P₁ Dn ® 0

(4.45)

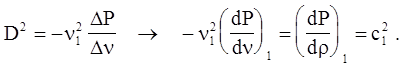
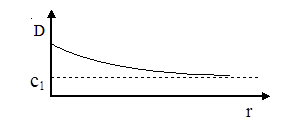Рис. 4.11

Таким образом, ударная волна на большом удалении от места ее возникновения в пределе превращается в звуковую волну, при этом скорость ударной волны стремится в

пределе к скорости звука (рис. 4.11).

Уравнение Гюгонио для ударной волны

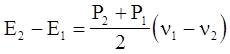
в пределе при P₂ ® P₁ принимает вид

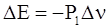или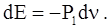

Сравним полученное выражение с первым началом термодинамики

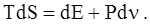
Очевидно, что полученное нами выражение для ударной волны в виде

dE + Pdn = 0

представляет собой первое начало термодинамики, в котором dS = 0 или S = const. Иными словами, ударная волна на большом расстоянии от места своего возникновения в пределе превращается в изоэнтропическую звуковую волну.

Удобно выразить основные параметры ударной волны u₂, P₂, r ₂, как функции скорости звука с₁ невозмущенной среды:

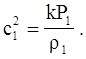(4.46)

Опустим все выкладки, запишем эти выражения уже в конечном виде

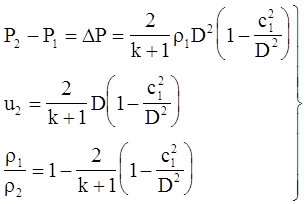(4.47)

Эти уравнения годятся и для сильных ударных волн (P₂ >> P₁, 1 >> c₁²/D²), и для слабых ударных волн (P₂ » P₁, c₁ » D).

Для сильной ударной волны при условии, что 1 >> c₁²/D² из уравнений (4.47) получим уравнения (4.41) и (4.44). Для слабой ударной волны, где 1» c₁²/D², получим из уравнения (4.47)

P₂ ® P₁, u₂ ® 0, r ₂ ® r ₁.

Дата добавления: 2014-01-04