Теорема о полном разложении определителя

Запишем k- ю строку определителя матрицы А в виде А_k=(а_k1,а_k2,…,а_kn)=а_k1(1,0,0,…,0)+а_k2(0,1,0,…,0)+а_kn(0,0,…,1)= = а_k1E₁ + а_k2E₂ +…+ а_knE_n = , k = 1,…, n, где

Е_s = (0,..,0,1,0,…,0) – здесь 1 стоит на s –м месте. Тогда

|A| = det (А₁ ,…, А_n) = det (,…,) =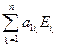

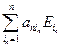=, и в этой сумме из пⁿ слагаемых все слагаемые, у которых существуют одинаковые индексы i_p= i_q, равны нулю, так как определители

det (E,E,…,E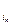) с одинаковыми строками 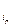E= E равны нулю. Следовательно, можно считать, что

|A| ==,

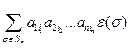где все индексы i₁,…,i_n в слагаемых различны, то есть образуют перестановку чисел 1,…,п; число слагаемых, следовательно, равно п!; e(s) = det (E,E,…, E), а

s =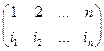 - подстановка.

Утверждение. e(s)=+1, если s - четная, и e(s) = - 1, если s - нечетная.

Доказательство. Очевидно, матрица со строками

E,E,…, E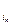 получается из единичной матрицы Е при помощи действия на столбцы подстановкой s. По утверждению из 3.2, если количество инверсий в нижней строке подстановки s равно m, то s можно разложить в произведение m транспозиций. И столбцы в матрице Е можно либо переставить все сразу с помощью s, либо переставить за m шагов, переставляя при помощи транспозиций каждый раз только два столбца. Так как при каждой перестановке столбцов определитель меняет знак, то e(s) = det (E,E,…, E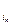)= (- 1)^m. Следовательно, если m - четно, то e(s) = + 1, а если m - нечетно, то e(s) = - 1.



Следствие. Если подстановку s можно разложить одним способом в произведение р транспозиций и другим способом в произведение q транспозиций, то четность p и q одинакова.

Доказательство. В самом деле, e(s)= det (E,E,…,E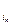)= = (- 1)^p =(- 1)^q Þ четность p и q одинакова.



Таким образом, нами доказана

Дата добавления: 2014-01-04