Основні поняття

Теорія автоматичного регулювання є складовою частиною науки про автоматичне керування технологічними процесами і використовує технічні засоби (регулятори). Завданням регулювання є утримання на заданому рівні регульованої величини (координати) або її зміна відповідно до прийнятої програми.

Регулювання це процес цілеспрямованого впливу на регульовану величину. Для цього регульовану величину перетворюють в сигнал зворотного зв’язку, з яким порівнюється сигнал завдання, і різниця між цими величинами служить для впливу (дії) на зміну регульованої величини, щоб наблизити її значення до значення завдання (задавальної величини).

Під час купання під душем бажано, щоб вода мала певну сталу температуру (рис.12.1). Тобто тут регульованою величиною є температура води. На її величину можна впливати встановленням відповідного положення головки крану-змішувача. При цьому бажано, щоб встановлена температура води (реальне значення регульованої величини) була якомога ближчою до заданого значення регульованої величини. Ці дії відповідають функціонуванню системи регулювання.

В системі регулювання завжди маємо справу із замкнутою структурою зі зворотним зв’язком за регульованою величиною.

Завади, які діють на систему регулювання, в даному випадку, наприклад, набирання кимось холодної води в сусідній кімнаті, спричинює виникнення різниці заданої величини і дійсної (похибка регулювання), тобто бажаної температури та її дійсного значення. Тому вентиль-змішувач, який є встановлювальним елементом системи, необхідно встановити (підкрутити) по-новому. Якщо це робити, надто різко повертаючи його головку, то вода – знаємо це з досвіду, - буде або загаряча, або захолодна. Тобто зміна температури матиме явно коливальний характер – отже, в системі регулювання є коливання. І тільки досвід, вивчення часу реакції температури води на зміни положення вентиля допоможуть встановлювати близьку до бажаної температуру води без значних її коливань.

В системах регулювання можуть виникати коливання.

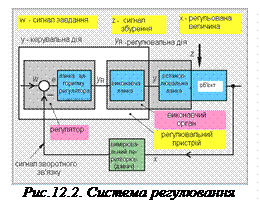
В технічному варіанті систем регулювання значення регульованої величини x вимірюється за допомогою відповідного сенсора (вимірювального перетворювача), і це виміряне значення віднімається від заданого значення w задавальної величини (рис.12.2). Похибка регулювання e = w - x 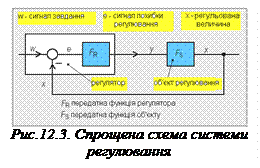перетворюється за допомогою регулятора в керувальну величину (дію) зі значенням y _R, яка керує виконавчою ланкою. Вихідною величиною виконавчої ланки є керувальна величина. Керувальна величина із значенням y впливає на значення регульованої величини x за допомогою встановлювального елементу, який є вхідною частиною об’єкту регулювання. Регульована величина x є виходом об’єкту регулювання.

В усталеному режимі систем регулювання похибка регулювання дуже мала або дорівнює нулеві. Поява завад або зміна значення задавальної величини (зміна завдання) викликають зміну регульованої величини та збільшення похибки регулювання, яка компенсуватиметься завдяки зміні значення керувальної дії y об’єктом регулювання. Для уникнення коливань в системі не треба допускати надто різких змін керувальної дії.

У наведених спрощених схемах систем регулювання (рис.12.3) виконавчий елемент об’єднують із встановлювальним елементом в один виконавчий пристрій або встановлювальний елемент об’єднується з об’єктом регулювання (рис.12.2). Часто в цих схемах виконавчий елемент не виокремлюють, а на структурній схемі показують, що регулятор діє безпосередньо на об’єкт регулювання за допомогою керувальної (або регулювальної) величини y.

Отже, система регулювання в спрощеному вигляді складається з регулятора та об’єкта регулювання.

Види регулювання.

Системи регулювання в загальному поділяються на (рис.12.4):

• системи ручного регулювання, в яких хоча б один елемент системи регулювання задається вручну,

• системи автоматичного регулювання, які працюють без втручання людини, за винятком ручного введення заданого завдання.

Далі також розрізняють:

• системи стабілізації, а також

• системи стеження (слідкувальні).

Прикладом системи стабілізації є регулювання положення лазерного інструменту (рис.12.5), необхідне для забезпечення заданої, сталої для даного інструменту, відстані кінчика лазера від оброблюваної поверхні. Для фокусування лазерного променя точно на цій поверхні відстань d (регульована величина) неперервно вимірюється ємнісним сенсором і за допомогою гідравлічного рушія (виконавча ланка системи регулювання), встановленого на роботі, відразу ж коректується, як тільки d_дійсн відрізняється від d_зад.

В системі стабілізації регулятор намагається утримати дійсне значення регульованої величини на рівні заданого значення.

Завади, які діють на об’єкт регулювання, викликають лише тимчасові, перехідні відхилення дійсного значення від заданого.

Прикладом системи стеження є позиціювання (регулювання положення) полозків супорту різця токарного верстату (рис. 12.6) і (рис.12.7). Інструмент повинен швидко і точно відстежувати задане значення положення x _зад, біжуче значення якого задає система числового програмного керування (ЧПК) верстата. Завданням регулятора положення є обчислення біжучого значення похибки стеження x = x _зад – х _дійсн та генерування сигналу регулювання швидкості подачі v_x = K_vx• Δx (рис. 12.8). Привід подачі переміщує полозки осі руху X так, щоб похибка стеження дорівнювала нулю. Параметр K_vx називається підсиленням за швидкістю системи стеження положення.

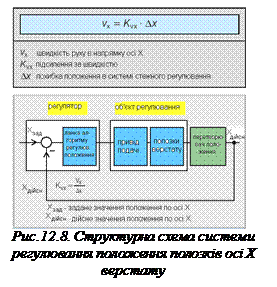
Чим більшим є значення підсилення за швидкістю, тим сильніше система регулювання реагує на похибку стеження. Для значення K_vx = 50 мм/с/мм полозки машини переміщуються при похибці стеження Δx = 1 мм із швидкістю V_x = 50 мм/c, a при похибці Δx = 0,1 мм – із швидкістю V_x = 5 мм/с. Якщо взяти значення підсилення за швидкістю дуже великим, то в системі може бути значне перерегулювання – перевищення заданого значення положення. Похибка стеження при цьому змінить свій знак і призведе до зміни знаку швидкості руху. Це означає, що перехідні процеси швидкості і положення матимуть коливний характер. В таких випадках кажуть, що система регулювання стає нестабільною.

Для полозків осі Z потрібна така сама, як і для осі X, система регулювання стеження положення.

В системі стеження регулятор забезпечує стеження (слідування) за значенням регульованої величини згідно до зміни заданої величини.

Для цього випадку регулювання завади та зміни завдання викликають також лише перехідні відхилення дійсної величини від заданої.

Завдання проектувальника системи регулювання полягає в оптимальному виборі регулятора та у визначенні його оптимальних налаштувань. При виборі регулятора і розрахункові його налаштувань потрібно враховувати динамічну поведінку системи регулювання, тобто характер перехідних процесів та значення підсилень кожної ланки системи. Крім коефіцієнтів підсилення, її динамічна поведінка також визначається такими параметрами, як сталі часу ланок та їх граничні частоти. Динаміка, а кажучи загальніше, здатність реагування даної системи, є тим кращою, чим меншими є сталі часу ланок і чим більші їх граничні частоти. Підсилення ланок визначається коефіцієнтами пропорційності і позначається переважно як K, або кутом нахилу реакції виходу ланки на стрибкоподібний вхідний сигнал.

Для створення системи регулювання та розрахунку її налаштувань потрібно знати статичні і динамічні властивості елементарних ланок, з яких складаються такі системи.

Ланки систем автоматичного керування

Властивості ланок систем керування визначаються такими їх показниками:

• зміна в часі (реакція) вихідної координати ланки при стрибкоподібній зміні вхідного сигналу,

• зміна в часі (реакція) вихідної координати ланки на синусоїдальний вхідний сигнал, а також

• амплітудна і фазова характеристики (т. зв. діаграма Боде).

Пропорційна ланка (ланка П)

Для пропорційної ланки її вихідний сигнал S₂ пропорційний до вхідного сигналу (вимушення) S₁ (рис. 12.9). У рівнянні залежності вихідного сигналу ланки S₂ від вхідного S₁ величина K_p є коефіцієнтом пропорційності або коефіцієнтом підсилення. K_р називають коефіцієнтом підсилення навіть тоді, коли він менший від 1, тобто коли має місце не підсилення, а послаблення дії.

Прикладами пропорційних ланок є коробки швидкостей (рис. 12.10), які змінюють швидкість обертання та момент, електронні підсилювачі, а також більшість сенсорів – вимірювальних перетворювачів, наприклад, тахогенератор для вимірювання кутової швидкості.

Якщо процеси розглядати докладніше (точніше), то ми побачимо, що кожна ланка системи керування реагує на зміну вхідного сигналу з деяким запізненням. Але якщо ці запізнення набагато менші, ніж запізнення інших ланок систем регулювання, наприклад, як запізнення сигналу сенсора кутової швидкості порівняно із запізненням (інерційністю) самого двигуна, то такі ланки називаються безінерційними.

Реакцією пропорційної ланки на стрибок вхідного сигналу буде стрибок вихідного сигналу. На схемах пропорційні ланки умовно позначаються стрибком вихідного сигналу (рис. 12.9).

Визначення коефіцієнта пропорційності K _p

Для визначення величини K_p потрібно мати математичне рівняння, яке описує залежність між вихідною S₂ та вхідною S₁ координатами. Якщо ця залежність невідома, то значення K_p можна визначити з статичної характеристики ланки або експериментально.

Значення сигналів S₂ i S₁, як правило, є нормованими, тобто позбавленими фізичних розмірностей. Нормовані значення отримують шляхом ділення значення реального фізичного сигналу на певну базову його величину, наприклад, на середнє або номінальне його значення.

Інерційна ланка першого порядку.

Вихідний сигнал інерційної ланки S₂ є пропорційним до вхідного сигналу S₁ лише після певного часу (рис. 12.11). Поведінка інерційної ланки описується двома параметрами – коефіцієнтом пропорційності (коефіцієнт підсилення) K_р та сталою часу Т. Реакція інерційної ланки S₂ на стрибкоподібний вхідний сигнал (вимушення) S₁ є показниковою функцією, а саме S₂ = K_р [1 - exp (-t/Т)]. Величина exp (- t/T) після часу t = 3T прямує до нуля, і вихідний сигнал S₂ стає пропорційним до вхідного сигналу S₁.

Прикладами інерційних ланок першого порядку є всі ті пристрої, в яких має місце накопичення енергії вхідного сигналу, наприклад, електричної енергії в конденсаторі чотириполюсника RC або кінетичної енергії маси ротора електродвигуна, який обертається, після зміни напруги керування.

Інерційні ланки першого порядку характеризуються накопиченням енергії та сталою часу.

Реакцією інерційної ланки першого порядку на синусоїдальний вхідний сигнал сталої частоти є, після перехідного процесу, також синусоїдальний сигнал тієї ж частоти, але з іншою амплітудою і фазою, ніж сигнал входу (рис. 12.12). Для високих частот амплітуда вихідного сигналу відчутно зменшується, бо накопичення енергії не встигає за черговими періодами її надходження та відбору. Інерційні ланки першого порядку згладжують високочастотні пульсації вхідних сигналів.

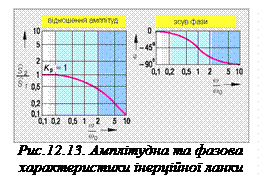
У зв’язку з цим інерційні ланки 1-го порядку також називають фільтрами низьких частот, бо вони пропускають сигнали, які змінюються повільно, і гасять сигнали високих частот (рис. 12.13). Високі частоти відповідають співвідношенню ω/ω₀ > 1, тобто ω = 2 πf > ω₀ = 2 π f₀, низькі - співвідношенню ω/ω₀ < 1, тобто ω = 2 π f < ω₀ = 2 π f₀. Частота пульсацій (кутова частота) ω₀ = 2 π f₀ = 1/Т, яку називають частотою спряження або граничною, є одним з параметрів, які характеризують властивості інерційної ланки 1-го порядку. Внаслідок запізнення в часі вихідних сигналів по відношенню до вхідних інерційна ланка 1-го порядку зсуває фазу вихідного сигналу (рис.12.13). Кут фазового зсуву змінюється від φ = 0° для частоти ω = 0 до φ = - 90° для частоти ω →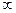. Для частоти спряження (граничної) ω = 2 π f₀ = ω₀ цей зсув становить φ = - 45° (рис. 12.13). Інерційні ланки 1-го порядку зсувають фази перехідних процесів виходу по відношенню до входу.

Інерційна ланка другого порядку і коливна ланка

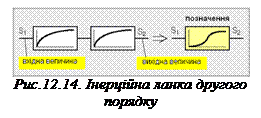
Інерційна ланка другого порядку складається з двох послідовно з’єднаних ланок 1-го порядку (рис. 12.14). Запізнений вихідний сигнал першої ланки 1-го порядку запізнюється ще й другою ланкою, яка також накопичує енергію. Відповідь виходу інерційної ланки другого порядку на стрибок вхідного сигналу (вимушення) має вигляд розтягненої літери S (рис. 12.14). Дотична до цього перехідного процесу в початковій точці є горизонтальною.

Коливна ланка також є поєднанням двох ланок, які накопичують енергію, але цю енергію вони то накопичують, то віддають. Внаслідок розсіювання енергії реакція виходу ланки 2-го порядку має коливний характер, але із вгамовуванням.

Параметрами, які описують коливну ланку, є частота невимушених коливань ω₀ = 2πf₀ та коефіцієнт вгамовування D. У випадку, коли D = O, коливання не вгамовуються, в межах значень коефіцієнта O < D < 1 – вони вгамовуються, а якщо D > 1 – тоді ланка перетворюється в інерційну ланку другого порядку.

Реакцією інерційної ланки 2-го порядку та коливної ланки на синусоїдальний вхідний сигнал (вимушення) є також синусоїда (рис. 12.15). Для вимушень з дуже низькою частотою ω << ω₀ = 2 π f₀ амплітуда вихідного сигналу збільшується пропорційно до значення коефіцієнта K_p (рис. 12.16). Для вимушень з дуже великою частотою ω >> ω₀ = 2 π f₀ амплітуда вихідного сигналу стає дуже малою – в цьому діапазоні величина амплітуди вихідного сигналу Ŝ₂ зменшується пропорційно до 1 / ω ².

Для частоти вимушення, що дорівнює частоті невимушених коливань, тобто ω = ω₀ = 2 π f₀ амплітуда вихідного сигналу стає дуже залежною від коефіцієнта вгамовування D (рис. 12.16) – її величина визначається із залежності Ŝ₂ = K_p/(2D), наприклад, для D = 0,5 її значення є в K_р разів більше від амплітуди вхідного сигналу. Інерційна ланка 2-го порядку і коливна ланка зсувають фазу вихідного перехідного процесу по відношенню до вхідного (рис. 12.16). Фазовий кут змінюється від φ = 0° для частоти ω = O до φ = -180° для частоти ω →∞. Для частоти спряження (граничної) ω = ω₀ = 2 π f₀ зсув фаз становить φ = -90°. Кут зсуву фаз залежить від коефіцієнта вгамовування D.

Інерційні ланки 2-го порядку, так само як і першого, використовуються як низькочастотні фільтри (другого порядку). Вони сильніше, ніж фільтри 1-го порядку, гасять частоти понад f₀. Коливні ланки з малим коефіцієнтом вгамовування використовуються як осцилятори, наприклад, для вимірювання часу. В кварцевих годинниках вони генерують частоти порядку багатьох МГц.

В коливних ланках відбувається обмін енергії між двома накопичувальними елементами.

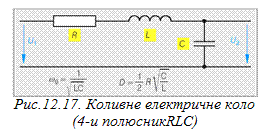
Коливні ланки можуть бути як механічними, так і електричними – їх можна створити, наприклад, на основі чотириполюсників RLC (рис. 12.17).

Інтегрувальна ланка (І)

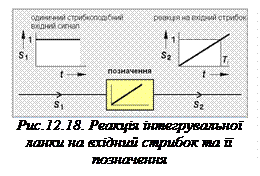
В інтегрувальній ланці (ідеальній) вихідний сигнал є пропорційним до інтегралу за часом від сигналу входу (рис. 12.18). Під цим розуміють біжуче додавання значень вхідного сигналу в “чергові” моменти часу. Стала часу інтегрування T_і це час, за який вихідний сигнал досягає величини стрибка вхідного сигналу (вимушення) (рис. 12.18). Обернена величина до сталої часу T_і називається коефіцієнтом інтегрувального підсилення і позначається як K_і (K_і = 1/ T_і).

S₂ вихідний сигнал

T_і стала часу інтегрування

K_і коефіцієнт інтегрувального підсилення

t час

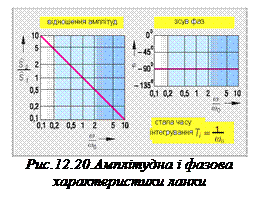
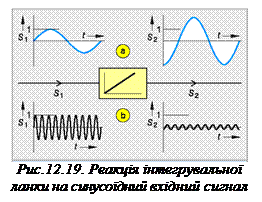На синусоїдне вимушення ланка І відповідає також синусоїдним перехідним процесом (рис. 12.19). При малих частотах, тобто при ω << ω₀ = 1/ T_і амплітуда вихідного сигналу набагато більша від амплітуди вимушення. А для великих частот, тобто при ω >> ω₀ = 1/ T_і, вона набагато менша (рис. 12.19). З амплітудної характеристики можна встановити, що для частоти ω = ω₀ обидві амплітуди, вхідна і вихідна, рівні між собою (рис. 12.20). Зсув фаз в інтегрувальній ланці завжди сталий і рівний φ = -90°, тобто вихідний сигнал слідує за вхідним сигналом зі сталим кутовим запізненням.

Інтегрувальні ланки утворюються об’єктами, в яких відбувається перетворення:

• швидкості руху в переміщення (положення),

• прискорення у швидкість,

• швидкості двигуна в кут повороту (кутове положення),

• протікання якоїсь рідини у рівень наповнення ємності,

• електричного струму в електричний заряд конденсатора,

• частоти імпульсів у покази лічильника імпульсів.

У зв’язку з цим, якщо в системі приводу подачі верстата вхідною величиною прийняти швидкість обертання двигуна, а вихідною – переміщення (положення) стола верстата, то ця система має інтегрувальні властивості – вона є інтегрувальною ланкою. Те саме можна сказати і про електричний лічильник імпульсів, для якого частота імпульсів є вхідною величиною, а його стан – вихідною, і про резервуар – з вихідним рівнем наповнення та вхідним – допливом рідини через вхідний вентиль (рис. 12.21).

Диференціювальна ланка (Д)

В диференціювальній ланці (ідеальній) вихідний сигнал пропорційний до похідної від вхідного сигналу за часом. Під поняттям похідної розуміють крутизну зміни сигналу. Відповіддю ланки Днаодиничний вхідний стрибок є одиничний імпульс на її виході в момент цього стрибка (рис. 12.22). Якщо вхідний сигнал (вимушення) наростає за лінійним законом, то відповіддю диференціювальної ланки є стала величина.

Ланки Д можуть використовуватися як операційні підсилювачі, як перетворювачі аналогових сигналів, генерованих різноманітними сенсорами. Так якщо сенсор генерує сигнал, пропорційний до переміщення, то на виході ланки Д буде сигнал, пропорційний до швидкості руху, v_x = dx/dt.

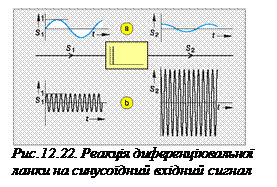Реакцією диференціювальної ланки на вхідний сигнал є, як і у попередніх ланках, синусоїдальний процес (рис. 12.22). Його амплітуда залежить від частоти вхідного сигналу. З амплітудної характеристики видно, що для частот ω < ω₀ амплітуда вихідного сигналу є меншою від амплітуди вимушення (рис. 12.23). Для частоти входу ω = ω₀ = 1/ T_d (T_d – стала часу диференціювання) обидві амплітуди однакові, а для ω > ω₀ вихідна амплітуда більша, ніж вхідна (рис. 12.23).

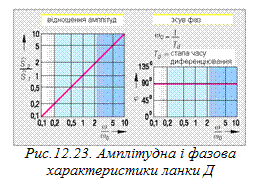Зсув фази в диференціювальній ланці завжди однаковий і рівний φ = +90°, тобто вихідний сигнал випереджує вхідний. Диференціювальні ланки підсилюють сигнали високих частот.

Ланка запізнення (T_t)

В ланці запізнення вихідний сигнал (відповідь) з’являється на її виході не в момент подачі вимушення, але лише через певний час, який називається часом запізнення (затримання) T_t. Сигнал-відповідь ланки запізнення повторює вхідний сигнал – на стрибок відповіддю є стрибок, але зі зміщенням у часі (рис.12.24).

Ланки запізнення використовуються в комп’ютерних перетвореннях даних.

Комп’ютер читає і перетворює тактовані сигнали, тому має місце запізнення чергових кроків на один такт.

Іншими прикладами ланок запізнення є всі об’єкти, в яких вихідна координата з’являється через певний час після подачі сигналу входу.

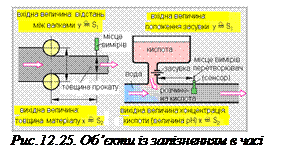Затримка в часі має місце, наприклад, при вимірюванні товщини прокату або при перемішуванні текучих рідин (рис.12.25).

На синусоїдальне вимушування ланка запізнення відповідає відповідає теж синусоїдальним сигналом з фазовим зсувом. Цей зсув становить φ = -360°, якщо час запізнення T_t дорівнює періодові вхідної синусоїди. Для частот вимушення ω₀ = 2 π f₀ = 1/ T_t зсув фази дорівнює φ = -360°/2 π = -57,3° (рис. 12.26).

Сумісна поведінка ланок, об’єднаних в систему регулювання

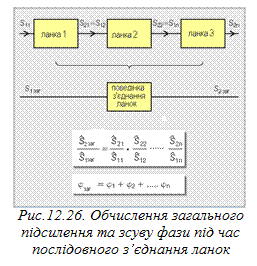В системах регулювання сигнали проходять від однієї ланки до іншої. Вихідний сигнал однієї ланки є входом для наступної (рис. 12.26).

Коефіцієнт підсилення послідовно з’єднаних ланок є добутком коефіцієнтів підсилення кожної з них. Якщо коефіцієнт підсилення однієї ланки Ŝ₂₁/Ŝ₁₁ = 2, а другої Ŝ₂₂/Ŝ₁₂ = 1,2, то загальний коефіцієнт підсилення буде рівний Ŝ_2заг · Ŝ_1заг = 2 ·1,2 = 2,4. Підсилення у більшості випадків залежить від частоти. Це означає, що для визначення загального підсилення потрібно розглядати значення підсилень з’єднаних ланок для одної певної частоти. Зсув фази послідовного з’єднання ланок дорівнює сумі зсувів фази кожної ланки.

Дата добавления: 2014-01-04