Решение матричных уравнений

Рассмотрим матричное уравнение АХ = В, где А – (п,п)- матрица с |A| ¹ 0, В - (п,т)- матрица, а Х – неизвестная (п,т)- матрица. Покажем, что существует единственное решение этого уравнения.

1. Пусть решение Х₀ $, то есть АХ₀= В. Тогда А^-1АХ₀=А^-1В Þ Х₀ = А^-1В - это означает единственность решения.

2. Подставим Х₀ = А^-1В в наше уравнение. Получим А(А^-1В) = АА^-1В = ЕВ = В, то есть Х₀ = А^-1В является решением уравнения. Это означает существование решения.

Покажем, как на практике можно решать матричные уравнения. Как мы видели в 9.3 при |A| ¹ 0 существуют элементарные матрицы Р₁, Р₂,…,Р_r такие, что P_r … P₂P₁A = D = =diag(d₁,…,d_n). Умножая это равенство слева на элементарные матрицы III-го типа P₁(d₁ ^-1), P₂(d₂ ^-1),…,P_п(d_п ^-1), получим

P₁(d₁ ^-1)P₂(d₂ ^-1)…P_п(d_п ^-1)P_r … P₂P₁A = Е. Таким образом, мы видим, что существуют элементарные матрицы Р₁, Р₂,…,Р_q такие, что P_q … P₂P₁A = E. Следовательно, P_q … P₂P₁ = А^-1. Отсюда можно получить два вывода.

1. А^-1= P_q … P₂P₁E, то есть для нахождения обратной матрицы надо над строками матрицы Е проделать те же ЭП, что проделывались над строками матрицы А при приведении её к единичной матрице Е. На практике это делают так: записывают матрицу вида (А|Е), и над «длинными» строками этой матрицы делают ЭП так, чтобы слева получилась матрица Е. Тогда справа получится матрица А^-1.

2. Для матричного уравнения АХ =В решение Х₀ = А^-1В = =P_q … P₂P₁В. Значит, для нахождения Х₀ надо над строками матрицы В проделать те же ЭП, что проделывались над строками матрицы А при приведении её к единичной матрице Е. То есть над «длинными» строками матрицы (А|В) надо делать ЭП так, чтобы слева получилась матрица Е. Тогда справа получится матрица А^-1В.

Теперь рассмотрим матричное уравнение YA = В, где А – (п,п)- матрица с |A| ¹ 0, В - (т,n)- матрица, а Y – неизвестная (т,n)- матрица. Как и ранее, можно показать, что существует единственное решение Y= BA^-1 этого уравнения. На практике решать такие матричные уравнения можно двумя способами. 1-й способ – это транспонировать наше уравнение: (YA)^t = A^tY ^t = В ^t, найти, как и ранее, с помощью ЭП над «длинными» строками решение X матричного уравнения A^tХ = В ^t, и затем получить Y = Х ^t.

2-й способ заключается в следующем. Матрицу А с |A|¹ 0 можно привести к единичной не только элементарными преобразованиями над строками, но также и аналогичным образом элементарными преобразованиями над столбцами. То есть существуют элементарные матрицы Р₁, Р₂,…,Р_t такие, что AP₁P₂ … P_t = E. Следовательно, P₁P₂ … P_t = А^-1, и А^-1 = EP₁P₂ … P_t, то есть для нахождения обратной матрицы надо над столбцами матрицы Е проделать те же ЭП, что проделывались над столбцами матрицы А при приведении её к единичной матрице Е. На практике это делают так: записывают матрицу вида 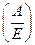, и над «высокими» столбцами этой матрицы делают ЭП так, чтобы сверху получилась матрица Е. Тогда снизу получится матрица А^-1.

Для матричного уравнения YA = В решение Y = BA^-1 = =ВP₁P₂ … P_t получается проделыванием над столбцами матрицы В тех же ЭП, которые проделывались над столбцами матрицы А при приведении её к единичной матрице Е. На практике это делают так: записывают матрицу вида 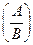, и над «высокими» столбцами этой матрицы делают ЭП так, чтобы сверху получилась матрица Е. Тогда снизу получится матрица ВА^-1.

Дата добавления: 2014-01-04