Доказательство. Пусть j : L ® L¢ - линейное отображение

Теорема 1.

Определения.

ОБРАЗ И ЯДРО ЛИНЕЙНОГО ОТОБРАЖЕНИЯ

Пусть j: L ® L^¢ - линейное отображение.

1. Образом линейного отображения j называется множество Imj = {y Î L^¢ |$ xÎ L: y = j x}, то есть Imj = {jx| x Î L} =

= jL Ì L^¢.

2. Ядром линейного отображения j называется множество Kerj = {xÎ L| j x = 0}, то есть Kerj = j ^-1(0_L¢)Ì L.

1. Imj - подпространство в L^¢.
2. Kerj - подпространство в L.

Эта теорема – частный случай теоремы 2.

Теорема 2. Пусть j: L ® L^¢ - линейное отображение, V –

подпространство в L, W – подпространство в L¢. Тогда j V - подпространство в L¢, j ^-1W – подпространство в L (образы и прообразы подпространств при линейных отображениях яв­ляются подпространствами).

Доказательство.

1. Пусть y₁, y₂ÎjV Þ $ х₁, х₂Î V такие, что y₁=jх₁, y₂=jх₂.

"a,bÎ Р aх₁+bх₂ÎV, так как V – подпространство Þ j(aх₁+bх₂)=aj х₁+bj х₂= a у₁+b у₂ÎjVÞ jV - подпростран­ство.

2. Пусть х₁, х₂Î j ^-1W Þ jх₁, jх₂Î W Þ "a,b Î Р

aj х₁+bj х₂ = j(aх₁+b х₂) Î W, так как W – подпространство Þ aх₁+bх₂Î j ^-1W Þ j ^-1W - подпространство.

ÿ

Теорема 3. j - инъекция Û Kerj = {0}.

Þ. Если Kerj ' х ¹ 0, то j х = j 0 = 0Þ j - не инъекция.

Ü. Если j х₁= j х₂, то j х₁ - j х₂= j (х₁ – х₂)= 0 Þ

х₁ – х₂Î Kerj = {0} Þ х₁ – х₂= 0 Þ х₁ = х₂ Þj - инъекция.

ÿ

Замечание. Kerj - мера неинъективности отображения

j: если y =j х, то j ^-1y = х + Kerj.

Доказательство.

1. j (х + Kerj)= j х +j(Kerj)=у + 0 = у Þ j ^-1y Ê х + Kerj.

2. Если х¢Î j ^-1y, то j х¢ = j х = у Þ j(х¢ - х) = 0

Þ х¢ - х Î Kerj Þ х¢ Î х + Kerj Þ j ^-1y Í х + Kerj.

ÿ

Теорема 4 (структура Imj). Пусть j: L ® L^¢ - линейное

отображение, е = {е₁,…, е_n} – базис в L, е¢ = {е¢₁,…, е¢_m} – ба­зис в L¢, [ j ] - матрица j в базисах е, е¢. Тогда:

1. Imj = <j е₁,…,j е_n>,
2. dim Imj = rg [ j ].

Доказательство.

1. "xÎL, x=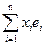, j х = j(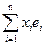)=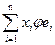Î<j е₁,…,j е_n>

Þ Imj = <j е₁,…,j е_n>, {jе₁,…,j е_n} – система образующих для Imj.

2. dim Imj - это ранг системы векторов {j е₁,…,j е_n}, то есть ранг системы столбцов координат этих векторов [ 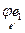] ,…, [ 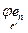], которые явля­ются столбцами матрицы [ j ]. Отсюда dim Imj = rg [ j ].

ÿ

Следствие. Так как в равенстве dim Imj = rg [ j ] левая

часть от базиса не зависит, то и rg [ j ] во всех базисах один и

тот же.

Определение. Пусть j: Lⁿ® L^m - линейное отображение. Рангом отображения j называется число dim Imj = rg [ j ], которое мы будем обозначать rgj.

Дефектом отображения j называется число dim Kerj, кото­рое мы будем обозначать defj.

Теорема 5. rgj + defj = n = dimLⁿ.

Доказательство. Выберем базис {е₁,…,е_d} в подпростран­стве Kerj и дополним его до базиса {е₁,…, е_d, е_d+1,…, е_n} всего пространства Lⁿ. Тогда Imj =<j е₁,…,j е_d, j е_d+1,…,j е_n>=

= <j е_d+1,…,j е_n>, так как j е₁=…=j е_d= 0. Покажем, что {j е_d+1,…,j е_n} – базис в пространстве Imj. Для этого достаточно доказать, что векторы {j е_d+1,…,j е_n} – линейно независимы. Пусть a_d+1j е_d+1 +…+ a_nj е_n = 0 Þ

j(a_d+1е_d+1+…+a_nе_n) = 0Þ

a_d+1 е_d+1 +…+ a_n е_n Î Kerj = <е₁,…, е_d> Þ

a_d+1е_d+1 +…+ a_nе_n=a₁е₁+…+a_d е_d Þ

a₁е₁+…+a_d е_d - a_d+1 е_d+1 -…-a_nе_n= 0. Но {е₁,…,е_n} линейно не­зависимы. Значит, все a _i= 0. Таким образом, {jе_d+1,…,j е_n} – базис в пространстве Imj, dim Imj = n – d = n – dim Kerj Þ

rgj + defj = n = dimLⁿ.

ÿ

Следствие. Lⁿ=<е₁,…, е_d, е_d+1,…, е_n>=<е₁,…, е_d> Å

Å <е_d+1,…, е_n>=Kerj Å <е_d+1,…, е_n>, и j: <е_d+1,…, е_n>® Imj - изоморфизм линейных пространств.

Лекция 27.

Теорема 6. Для линейного оператора j:Lⁿ ® Lⁿ эк­вива­лентны следующие 10 условий:

1. Kerj = {0},
2. defj = 0,
3. rgj = n,
4. Imj = Lⁿ,
5. j - инъекция,
6. j - сюръекция,
7. j - биекция,
8. $ j ^-1,
9. $ [ j ] ^-1,
10. detj ¹ 0.

Доказательство.

Очевидно, 1Û2 и 3Û4Û6 из определения, 2Û3 из тео-

ремы 5, 1Û5 из теоремы 3, 5&6Û7 из определения. Так как rgj = rg [ j ], а detj = det [ j ], то из теории определителей 3Û10, а из теории матриц 10Û9. Эквивалентность 9Û8 сле­дует из того, что [ j ] ^-1= [ j ^-1 ]. Либо можно доказать эквива­лентность 7Û8 следующим образом: 8Þ7 – из определения, а если имеет место 7, то, очевидно, отображение j ^-1$, и нам требуется лишь доказать его линейность. Пусть j ^-1х = u,

j ^-1y = v Þ j u = х, j v = y Þ j(a u+b v) =a х +b yÞ

j ^-1(a х +b y) = a u+b v = aj ^-1х + bj ^-1y Þ j ^-1 – линейно.

ÿ

Определение. Линейный оператор j называется невы­рожденным, если выполняется любое из десяти эквивалент­ных условий из Теоремы 6. В противном случае оператор называется вырожденным.

Дата добавления: 2014-01-04