Теорема 3 (про середню лінію). Середня лінія трикутника (лінія, що сполучає середини двох його сторін) паралельна третій його стороні і дорівнює її половині

Теорема 4. Середня лінія трапеції (лінія, що сполучає середини бічних її сторін) паралельна основам і дорівнює їхній півсумі (рис. 3).

Рис. 3

Задача. У трапеції ABCD паралельні сторони мають відповідно довжини ВР = 12, AD =20. Знайти довжини трьох відрізків, на які діагоналі АС і BD поділяють середню лінію трапеції (рис. 4).

Ø МР — середня лінія Δ АВС. Тому за теоремою 2 маємо:

2. QN — середня лінія Δ ВDC; відповідно

3. MN — середня лінія трапеції ABCD, тому за теоремою 3 маємо: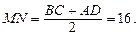

4. PQ = MJV – MP – NQ = 16 – 6 – 6 = 4. Дістаємо: МР = NQ = = 6, PQ = 4.

Рис. 4

Теорема 5 (про бісектрису внутрішнього кута трикутника). Бісектриса внутрішнього кута довільного трикутника поділяє протилежну сторону на відрізки, пропорційні до прилеглих сторін: 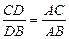(рис. 5, а).

Задача. У прямокутному трикутнику АВС (рис. 5, б) АС = 3, ВР = 4. Знайти довжини відрізків, на які бісектриса AD поділяє сторону ВС, а також довжину бісектриси AD.

Ø За теоремою Піфагора знаходимо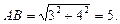

2. Нехай AD — бісектриса CAB. Позначимо CD = x, тоді
BD = 4 – x.

3. За теоремою 5 маємо 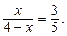Звідси

4. За теоремою Піфагора для CAB дістанемо AD ² = АС ² + + CD ². Тому Остаточно маємо:

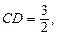
Рис. 5

Два трикутники називаються подібними, якщо їхні відповідні кути рівні, а відповідні сторони пропорційні.

Ознаки
подібності трикутників

Дата добавления: 2014-01-04