Побудова функції Гріна методом відображення зарядів для граничних задач оператора Лапласа

Для побудови функції Гріна оператора Лапласа використовується фізична інтерпретація фундаментального розв’язку тривимірного та двовимірного евклідового простору. Нагадаємо, що фундаментальний розв’язок оператора Лапласа має вигляд: (4.1)

Для тривимірного простору фізичний зміст фундаментально розв’язку нам відомий і представляє потенціал електростатичного поля в точці 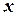одиничного точкового заряду, який розташований в початку координат. Для двовимірного випадку ми визначимо фізичний зміст фундаментального розв’язку трохи нижче.

Таким чином функцію Гріна для деякої просторової області можна шукати у вигляді потенціалу електростатичного поля сукупності точкових або розподілених зарядів, один з яких є одиничним і знаходиться в довільній внутрішній точці області 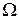, а усі інші лежать поза областю 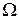, місце розташування і величина зарядів підбираються таким чином, щоби задовільними однорідним граничним умовам на поверхні області.

Тобто функція Гріна дуже часто може бути знайдена у вигляді:

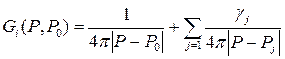(4.2)

У формулі (4.2) перший доданок є фундаментальним розв’язком і одночасно моделює потенціал в точці 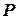одиничного точкового заряду розташованого в точці 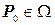.Сума - другий регулярний доданок, який фігурує в визначенні 2 функції Гріна представляє функцію 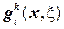, 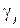-константи, які моделюють величину точкового заряду, 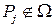- точки розташування зарядів, які лежать поза областю .

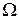Оскільки має місце рівність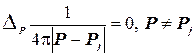, то сума 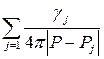в рівності (4.2) дійсно задовольняє рівняння Лапласа коли .

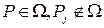Задача Дірихле для півпростору

Розглянемо граничну задачу:

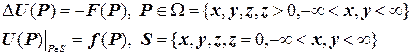(4.3)

Для знаходження розв’язку цієї задачі побудуємо функцію Гріна першої граничної задачі оператора Лапласа у півпросторі .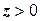

В довільній точці 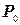верхнього півпростору розташуємо одиничний точковий заряд, потенціал якого обчислюється 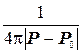, в нижньому півпросторі 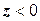, розташуємо компенсуючи заряди, так що би в кожній точці поверхні (площині 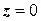) сумарний потенціал електростатичного поля дорівнював нулю.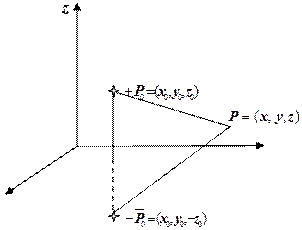

У зв’язку з принципом суперпозиції електростатичних полів, легко зрозуміти, що компенсація потенціалу вже розташованого заряду відбудеться у випадку, коли компенсуючий заряд розташувати дзеркально існуючому відносно площини 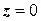, а величину заряду обрати одиничну з знаком мінус.

В результаті отримаємо сумарний потенціал електростатичного поля

(4.4)

Легко перевірити, що

Таким чином побудована функція (4.4) представляє собою функцію Гріна першої граничної задачі (Дірихле) оператора Лапласа для півпростору.

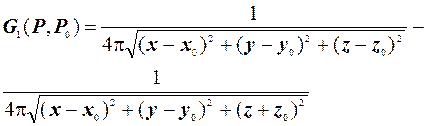(4.4’)

Для знаходження розв’язку задачі Діріхле скористаємося формулою інтегрального представлення (3.16)

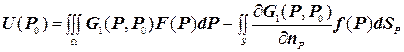
Обчислимо
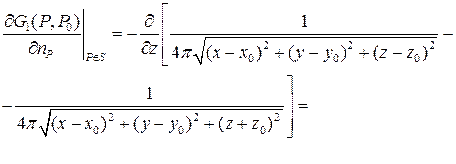
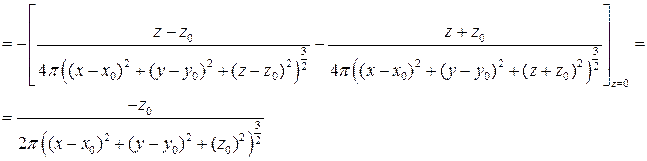Таким чином, використовуючи формулу інтегрального представлення можемо записати розв’язок задачі Дірихле для рівняння Пуассона:

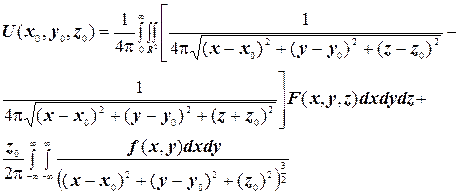(4.5)

Задача Неймана для півпростору

Будемо розглядати граничну задачу

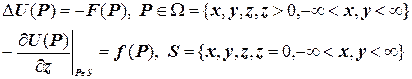(4.6)

Для розв’язання цієї задачі побудуємо функцію Гріна другої граничної задачі оператора Лапласа для півпростору.

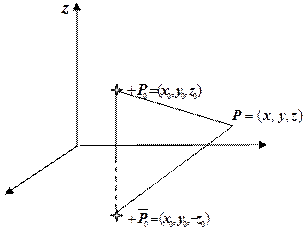Для випадку умови другого роду тобто коли на площині 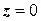виконується умова , її можна інтерпретувати як рівність нулю потоку електростатичного поля крізь площину .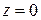

Це означає, що поле внутрішнього одиничного заряду треба компенсувати полем зовнішніх зарядів. Це можна зробити, якщо дзеркально одиничному позитивному заряду в точці 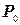розташувати заряд додатного знаку в симетричній точці 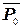. Таким чином сумарний потенціал двох зарядів, а значить і функцію Гріна можна записати у вигляді:

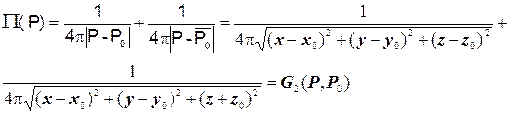(4.7)

Перевіримо, що побудована функція Гріна задовольняє граничній умові

Враховуючи формулу інтегрального представлення розв’язку другої граничної задачі (3.17), отримаємо формулу для розв’язку задачі Неймана рівняння Пуассона в півпросторі:

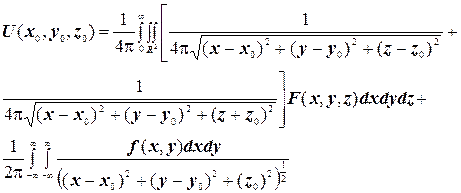(4.8)

Дата добавления: 2014-01-04