Определяются характеры каждой операции симметрии

Таким образом, в спектрах комбинационного рассеяния активны все четыре формы колебаний, из них две трижды вырожденные, одна является синглетной. Трижды вырожденные колебания являются активными и в спектрах инфракрасного поглощения.

До

Изменение колебаний, полученных в п.3, под влиянием симметрии поля кристалла.

Алгоритм Сайт-групповой анализ

Алгоритм анализа. Определяются:

1) внутренние колебания свободного оксианиона PO₄^3—, их типы, форма, симметрия и активность в ИК спектрах поглощения и спектрах КР;

2) сайт–группа симметрии (позиционная симметрия) оксианиона PO₄^3- в кристалле;

3) изменение внутренних колебаний свободного PO₄^3- оксианиона под влиянием поля сайт-группы;

На языке теории групп такая процедура сводится к переходу:

1) от неприводимых представлений группы симметрии тетраэдра (Td), свойственных свободным PO₄^3- –оксианионам,

к неприводимым представлениям симметрии сайт-группы;

2) от неприводимых представлений симметрии сайт-группы к неприводимым представлениям пространственной группы симметрии кристалла С²_6h.

Определение внутренних колебаний свободного оксианиона PO₄^3-

Внутренние колебания свободного PO₄^3- оксианиона определяются их тетраэдрической симметрией (Td) с елементами симметрии: четырьмя осями третьего порядка (4С₃), тремя осями второго порядка (3С₂) и шестью диагональными плоскостями симметрии (6δ_d).

Для определения внутренних колебаний: выписываются все неприводимые представления группы симметрии тентраэдра* по приведенным ранее формулам вычисляются характкры полного колебательного представления оксианиона PO₄^3-, которые разлагаются по формуле 2.50 по неприводимым представлениям группы ситмметрии тетоаэдра. Полученные данные сводятся в табл. 2.16

Табл.2.16 Разложение полного колебательного представления оксианионов конфигурации типа по неприводимым представлениям группы симметрии

		8	3	6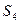	6
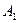
					1
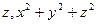
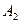
				-1	-1
		-1					3;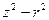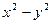
			-1		-1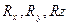
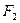
			-1	-1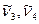
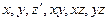
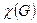
				-1

Из табл. 2.16 следует, что в спектрах поглощения активны только трехкратно-вырожденные колебания симметрии F₂, поскольку при этом типе симметрии изменяется дипольный момент (колебание будет активно в ИК-спектре поглощения, если хотя бы один из компонентов дипольного момента принадлежит к той же симметрии, что и соответствующая форма нормального колебания). В спектрах КР активными будут колебания 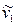_­(A₁), (E) и 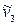, 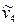_­(F₂), поскольку к этому уже типу симметрии принадлежат компоненты векторов поляризуемости.

Полученные 4 типа колебаний для свободных оксианионов PO₄^3— по форме и симметрии имеют вид покзазанный на рис.2.17

((

Рис. 2..17. Форма и симметрия нормальных колебаний тетраэдрических группировок оксианионов структурного типа XY₄

В табл.2.17 представлены экспериментальные результаты по частотам внутренних колебаний оксианионов PO₄^3-

Табл. 2.17 Частоты (см^-1) свободных оксианионов PO₄^3—, их активность в спектрах ИК поглощения и спектрах КР.

ион	1(A1) KP	2(E) KP	3(F2) ИК,KP	4(F2) ИК,KP
PO4^3-

В приведенных обозначениях символы А, Е, F означают однократно, двукратно, трехкратно вырожденные колебания, а s, as, δ – симметричные, ассиметричные, деформационные, соответственно.

В кристаллической решетке PO₄^3—оксианионы можно рассматриваются как свободные на которые действуют внутрикристаллические поля сайт – группы симметрии (позиционной симметрии) и симметрии решетки в целом.

Определение симметрии сайт-группы:

в кристаллической решетке симметрия оксианиона PO₄^3- понижается в результате до симметрии сайт-группы (области расположения иона); симметрия сайт-группы оксианиона PO₄^3- в кристалле гидроксилапатита находится из соображений, что она одновременно должна быть подгруппой групп симметрии тетраэдра (Td) свободной молекулы и симметрии кристалла(С²_6h)

Из анализа рис.2.18 и частных положений атомов следует, что позиционной группой симметрии PO₄^3- – иона в кристалах гидроксилапатита будет подгруппа групп симметрии Td и С²_6h, а именно, сайт-группа симметрии С_S.

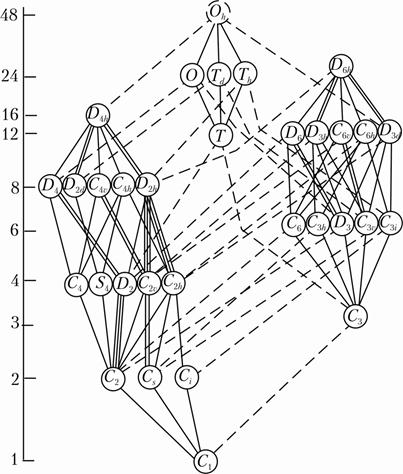
Рис.2.18 Соотношения между группами и подгруппами 32 кристаллографических точечных групп.

Соответствующий набор симметрийных позиций возможных расположений структурных единиц соединения в пространственной группе симметрии С²_6h. (табл. 1. Приложение 1), а именно– С₁(12), 3С_3h(2), С_3i(2), 2С₃(4), С_i(6), С_s(6), также подтверждает сделанный выбор.

Изменение колебательных состояний свободного PO₄^3- оксианиона симметрии Td под влиянием поля сайт-группы симметрии С_S, а затем и внутрикристаллического поля симметрии С²_6h, сводится к переходу от неприводимых представлений внутренних колебаний молекулярной группы симметрии Td к неприводимым представления сайт-группы симметрии С_S, а затем к неприводимым представлениям кристалла, к фактор-группе пространственной группы С²_6h. -С_6h.

Чтобы не делать математических вычислений результат такого перехода можно получить из корреляционной схемы (рис.2.18).

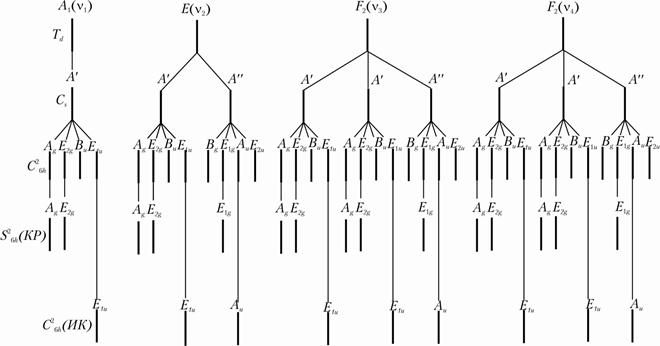
Рис.2.14. Корреляционная схема для оксианионов 6PO₄^3-– в кристалле апатита (С²_6h).

Как видно из рисунка 2,18 все вырождения снимаются и PO₄^3- –оксианион будет характеризоваться девятимерным неприводимым представлением.

Поскольку в элементарной ячейке гидроксилапатита шесть оксианионов PO₄^3-, то под действием кристаллического поля симметрии С²_6h произойдет шестикратное расщепление каждого терма с симметрией соответствующих пространственной группе С²_6h.

Колебательные представления частот, активные в спектрах ИК поглощения и спектрах комбинационного рассеяния представляются в виде:

Г_ν=6Ag(UK,KP)+3Au(UK)+3Bg(H.A)+6Bu(H.A)+3 E_1q(UK,KP)+6E_1u(UK) +6E_2q(KP)+3E_2u(H.A)

Следовательно:

54 колебаний шести PO₄^3- – ионов могут проявиться: в 9-ти частотах активных в спектрах ИК поглощения и спектрах КР; в 9-ти частотах активных только в спектрах ИК поглощения;

и в 6 – ти колебаниях активних только в спектрах КР.

2.15Фактор–групповой анализ колебательных спектров (метод Багавантама–Ванкатарайду).

Фактор–группой называется группа операций симметрии, которые образуются после замены в пространственной группе симметрии простых трансляций операцией идентичности Е

Для выполнения последовательного сайт–группового и затем фактор–группового анализов в большинстве случаев достаточно располагать сведениями:

о симметрии излучаемой молекулы (иона);

о симметрии пространственной группе кристалла;

о числе формульных единиц в элементарной ячейке кристалла.

Продолжим анализ колебательных спектров гидроксилапатита [Ca₅(PO₄)₃OH]:

Учитывая, что в элементарной ячейке гидроксилапатита содержится 2 формульные единицы Ca₅(PO₄)₃OH и координаты атомов в элементарной ячейке (табл. 2.19),то наиболее вероятными расположениями его атомов могут быть следующие сайт-группы симметрии: 4 СаI - в С₃(4); 6 CaII – в С_S(6); 2 OH – в С_3h(2); 6 PO₄^3- –в С_S(6); 6 P – в С_S(6); 6 OI – в С_S(6); 6 OII – в С_S(6); 12 OIII – в С₁(12).

Табл. 2.19. Координаты атомов гидроксилапатита [Ca₅(PO₄)₃OH] в элементарной ячейке

Атомы	Число атомов на элементарную ячейку	координаты
X	Y	Z
CaI		0,333	0,667	0,001
CaII		0,246	0,993	0,250
P		0,400	0,369	0,250
OI		0,329	0,484	0,250
OII		0,589	0,446	0,250
OIII		0,348	0,259	0,073
OH		0,000	0,000	0,250

О типах структурных единиц:по литературным данным, катионы кальция СаI иСаII различают тем, что они занимают две различные позиции: на оси С₃ и в зеркальной плоскости симметрии, соответственно;длины связей определяют тип и место кислорода О, например: (Р–OI)–1,533Å, (Р–OII)–1,544Å, (Р–OIII)–1,514Å.

Анализ внутренних колебаний PO₄^3- проводится такой последовательности: записывается таблица характеров неприводимых представлений кристаллической группы симметрии С²_6h.; определяется количество атомов ячейки на операциях симметрии, не меняющих своих положений при действии операций данной группы, (так называемые, инвариантные атомы U_R(n_i) (количество инвариантных атомов и инвариантных групп сводится к определению их числа на элементах симметрии); определяются характеры соответствующих преобразований симметрии. Данные заносятся в табл.2.19 Количество инвариантных атомов и групп сводится к определению их числа на элементах симметрии:

Из табл. 2.19 следует, что для элементарной ячейки гидроксилапатита двумя формульными единицами 2 [Ca₅(PO₄)₃OH]:

общее число атомов = 44; число инвариантных групп р = 18 -[6PO₄, 4CaI, 6CaII, 2OH]; число инвариантных одноатомных групп (ν) = 14- [4CaI, 6CaII, 2О, 2H].

Число инвариантных атомов на элементах симметрии: на оси С₃ – 8(4CaI, 2О, 2H); на оси ₃ – 4(2О, 2H); в плоскости δ_h – 28 (6CaII, 6P, 6OI, 6OII, 2O, 2H);

Число инвариантных групп на элементах симметрии: на оси С₃ – 8(4CaI, 2O, 2H); на оси ₃ – 4(2O, 2H) в плоскости δ_h – 16 - (6PO₄ , 6CaII, 2O, 2H);

Число одноатомных инвариантных групп на элементах симметрии: на оси С₃ – 6(4CaI, 2O, 2H); на оси ₃ – 4(2O, 2H); в плоскости δ_h – 10(6CaII, 2O, 2H).

Для определения всех внутренних колебаний находятся сначала число атомов или групп атомов ячейки (n_i), не меняющих положения при действии данной операции симметрии (т.е. число инвариантных атомов U_R(n_i), затем по формуле

c_р®=U_R(±1+2cos) (2.46)

В (2.46) n и k – соответственно нижний и верхний индексы операции R; +1 берется для простого поворота, а –1 – для зеркального.

Произведением U_R(n_i) на c_р® находятся характеры полного колебательного представления.

Дата добавления: 2014-01-04