Лекція №16. Диференціальні рівняння вищих порядків

1. Основні поняття диференціальних рівнянь вищих порядків. Задача Коші

2. Лінійні диференціальні рівняння вищих порядків

3. Лінійні однорідні диференціальні рівняння із сталими коефіцієнтами

1. Основні поняття диференціальних рівнянь вищих порядків. Задача Коші

Розглянемо диференціальні рівняння, які містять похідні вищих порядків. Порядок найвищої похідної невідомої функції, що входить у диференціальне рівняння, називається порядком цього рівняння.

Диференціальне рівняння порядку має вигляд

, (1)

де - незалежна змінна, - невідома функція, - відома функція.

Рівняння (1), не розв’язане відносно старшої похідної , називається неявним диференціальним рівнянням.

Нормальним або явним диференціальним рівнянням порядку називається рівняння (1), розв’язане відносно похідної :

. (2)

Розв’язком рівняння (2) на деякому інтервалі 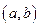називається разів неперервно диференційовна на цьому інтервалі функція , яка при підстановці в дане рівняння перетворює його в тотожність по .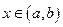

Графік розв’язку диференціального рівняння називається його інтегральною кривою.

Задача Коші: серед усіх розв’язків рівняння (2) знайти такий розв’язок , який при задовольняє такі умови (3), де - довільні наперед задані дійсні числа.

Умови (3) називаються початковими умовами рівняння (2).

Теорема Коші (про існування і єдиність розв’язку)

Якщо функція і її частинні похідні по аргументам неперервні в деякій відкритій області 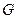, то для всякої точки 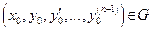існує єдиний розв’язок рівняння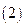, який задовольняє початкові умови(3).

2. Лінійні диференціальні рівняння вищих порядків

Рівняння виду , (4)

де 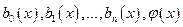- задані функції, називається лінійним диференціальним рівнянням порядку.

Функції 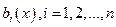, називаються коефіцієнтами даного рівняння, а функція - його вільним членом. Якщо вільний член дорівнює нулю, то рівняння (4) називається однорідним, якщо , то рівняння (4) називається неоднорідним.

Розглянемо лінійне однорідне диференціальне рівняння другого порядку

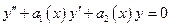(5)

Одним із розв’язків рівняння (5) є 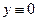, який називається нульовим або тривіальним.

Під задачею розв’язання однорідного диференціального рівняння розуміють задачу відшукання його нетривіальних розв’язків.

Дата добавления: 2014-01-04