В 1. Условия применения корреляционно-регрессион-ного анализа

Тема 6. Корреляционно-регрессионный анализ

1. Условия применения корреляционно-регрессионного анализа.

2. Этапы корреляционно-регрессионного анализа.

3. Виды парной корреляционно-регрессионной связи.

4. Парная линейная корреляционно-регрессионная модель.

5. Показатели тесноты связей линейной корреляционно-регрессионной модели.

6. Анализ достоверности парной линейной корреляционно-регрессионной модели.

7. Расчет параметров криволинейных уравнений.

8. Оценка тесноты связи при криволинейных моделях.

9. История развития многофакторного корреляционно-регрес-сионного анализа.

10. Расчет уравнения многофакторной корреляционно-регрес-сионной модели.

11. Оценка тесноты связи признаков и ранжир факторов по силе их влияния на результат в множественном корреляционно-регрессионном анализе.

12. Оценка достоверности результатов произведенного корреляционно-регрессионного анализа.

13. Прогнозирование по корреляционно-регрессионной модели.

14. Стандартизированный вид уравнения связи.

15. Рекомендации по составлению различных корреляционно-регрессионных моделей.

ЛИТЕРАТУРА:

1. Елисеева И.И., Юзбашев М.М. Общая теория статистики: М.: Финансы и статистика, 1998.

2. Ефимова М.Р., Рябцева В.М. Общая теория статистики. М.: Финансы и статистика, 1999.

3. Плошко Б.Г., Елисеева И.И. История статистики: Учеб.пособие / – М.: Финансы и статистика, 1990, – 295с.

4. Статистика сельского хозяйства. Под ред. Замосковного О.П., М.: Финансы и статистика, 1990.

5. Сельское хозяйство РБ: статистический сборник / ред.кол.: В.С. Метекс; В.Н. Синкевич; Л.Л. Выбчик и др.; Министерство статистики и анализа РБ. – Минск, 2006. – 223 с.

В курсе математики рассматриваются функциональные связи, где однозначно определяется значение одной переменной, если известно значение другой (или других). Многие экономические показатели связаны в жестко детерминированную систему, например, расчет уровня рентабельности затрат на производство и реализацию продукции. Однако в экономических и технологических явлениях часто значение одного показателя никогда не определяет однозначно значение другого показателя, хотя связь может наблюдаться. Например, уровень молочной продуктивности коров зависит от уровня кормления, аналогично уровень урожайности сельскохозяйственных культур зависит от доз органических и минеральных удобрений. В экономических исследованиях хорошо видно, что уровень себестоимости единицы сельскохозяйственной продукции зависит от уровня механизации производственного процесса, от уровня продуктивности биологического объекта (животных или земельных угодий) и т.д. Такая связь показателей называется стохастической или вероятностной и может быть установлена только при большом числе наблюдений.

«Corelation» – английское слово, введенное в употребление биологом и статистиком Френсисом Гальтоном (1822–1911) в конце ХIХ века. И переводится оно как «соответствие», т.е. нежесткая математическая зависимость.

Связь называется корреляционно-регрессионной, если значению результативного показателя соответствует несколько значений факторного признака, и, наоборот, при одном и том же значении факторного показателя можно достичь разных значений результата.

За результативный показатель в каждом конкретном анализе выбирается более важный признак, отражающий результаты деятельности. Например, объем валовой продукции, объем прибыли, уровень рентабельности, уровень себестоимости или цены единицы продукции. Для этих результативных показателей факторными могут быть: наличие основных производственных фондов, фондообеспеченность, фондовооруженность, производительность труда или трудоемкость, урожайность отдельных культур, продуктивность животных и т.д.

В другом примере результативным показателем может быть производительность труда, которая зависит от:

- уровня механизации производственного процесса;

- квалификации работников и т.д.

Корреляционно–регрессионная связь – это связь вариаций (изменений) различных показателей, когда изменение одного признака влияет на изменение другого признака.

Корреляционно-регрессионный анализ заключается в построении и анализе экономико-математической модели в виде уравнения регрессии и оценке тесноты связи между анализируемыми показателями. Поэтому принято отличать понятия «регрессия» и «корреляция». Очень часто в статистической литературе под регрессией понимают нахождение уравнения связи показателей, под корреляцией – определение тесноты связи изучаемых признаков.

В общем виде уравнение регрессии записывается в следующем виде:

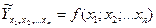(6.1)

где n – число факторов.

Условия применения корреляционно-регрессионного анализа:

1. Для построения корреляционно-регрессионной модели надо иметь достаточно большое количество значений каждого показателя, т.е. объем статистической совокупности должен содержать не менее 50 единиц.

2. Распределение значений анализируемых признаков у единиц совокупности должно быть близким к нормальному, т.е. сила вариации показателей должна быть минимальной.

Из второго условия вытекает требование отсутствия в анализируемой совокупности «аномальных» точек, т.е. таких значений признаков, которые сильно отличаются от большинства значений по всей совокупности. Аномальные точки должны быть удалены из анализируемой совокупности.

В 2. Этапы корреляционно-регрессионного анализа:

1. Предварительный (априорный) анализ. Он проводится достаточно квалифицированным исследователем и заключается в предварительном отборе (установлений) результативных и факторных показателей, которыми обладают единицы анализируемой статистической совокупности в соответствии с целью проводимого исследования.

2. Сбор информации и ее первичная обработка. Здесь выявляются ошибки наблюдения, информация проверяется на нормальность распределения показателей и отсутствие «аномальных» точек, иногда проводят группировку для предварительного установления связей.

3. Выбор вида и построение модели (уравнения регрессии) с использованием математического аппарата. Оценка уравнения регрессии на достоверность по одному из критериев достоверности.

4. Оценка тесноты связей признаков с использованием показателей, отражающих тесноту и направление связи (если его можно установить).

5. Прогнозирование развития явления по модели на перспективу.

На первом этапе формулируется задача исследования, определяется методика измерения показателей или сбора информации, исключаются дублирующие факторы или факторы, связанные в жесткую систему.

На втором этапе совокупность должна быть достаточно большой по числу единиц и наблюдений: N>>50, число факторов, влияющих на результат, должно соответствовать N. Данные должны быть количественно и качественно однородны.

На третьем этапе определяется внешний вид аналитической функции (уравнения регрессии) и находятся ее параметры.

На четвертом этапе оценивается достоверность всех характеристик корреляционно-регрессионной модели с использованием критериев достоверности (Стьюдента или Фишера).

На пятом этапе осуществляется прогноз усредненных значений показателей, наилучших значений и наихудших. По модели возможен ранжир единиц совокупности по влиянию факторного показателя на результативный.

Дата добавления: 2014-01-04