В 3. Виды парной корреляционно-регрессионной связи

К самым простым корреляционно-регрессионным связям относят парные или однофакторные связи. Среди парных выделяют: линейные и криволинейные связи. Результативный показатель обозначается У, факторный признак обозначается Х. Исходную базу данных (цифровую информацию) можно представить в виде горизонтальной или вертикальной таблицы. Например,

Таблица 6.1. База данных для исследования связи показателей

№ по порядку								N
Результативный показатель	У1	У2	У3					Уn
Факторный признак	Х1	Х2	Х3					Хn

В исходной информации вместо «№ по порядку» могут быть указаны наименования хозяйств (точек совокупности). Если задана информация в таком виде, то каждой паре чисел на декартовой системе координат в соответствие может быть поставлена точка. На рисунках 6.1 и 6.2 изображены некоторые виды таких графиков, которые называются точечными диаграммами.

Виды парной корреляционно-регрессионной связи:

1. Линейное уравнение регрессии:

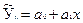
2. Степенная связь факторов:

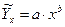или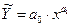

Это уравнение может быть приведено к линейному уравнению путем логарифмирования:

log Y = log a + b log х

3. Показательная связь факторов:

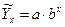
Уравнение приводится к линейному виду через логарифмирование:

log у = log a +(log b) х

4. Гиперболическая зависимость результата от фактора:

Ỹ_х= а +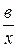

Это уравнение преобразуется в линейное уравнение подстановкой величины, обратной Х, т.е. Z=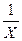

тогда Ỹ_z = a + bz.

Рисунок 6.1. – Прямая (положительная) регрессия

Рисунок 6.2. – Обратная (отрицательная) регрессия

5. Параболическая связь:

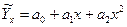
Дата добавления: 2014-01-04