Ряд динамики в виде произведения уравнения тренда на средние индексы сезонных колебаний

В 6. Модели рядов с учетом тенденции и сезонности.

Тенденцию ряда и наличие сезонности можно представить в виде двух различных моделей:

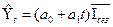(7.24)

Такого вида модель можно использовать, если есть информация помесячных или поквартальных данных за несколько лет. Последний год может быть полный, а может быть незавершенный. Тогда средние индексы сезонности должны быть рассчитаны с учетом имеющихся данных. В нашем примере рассматриваются квартальные данные за три полных года (таблица 7.12).

Используя данные столбцов t и У и метод наименьших квадратов в системе (7.12) найдем параметры уравнения тренда Ŷ=12,18–0,18t.

Таблица 7.12. Расчеты модели по данным квартальных отчетов.

Год	Квартал	t	Y	Тренд	I	Модель
	I		12,7	11,99808	1,058503	11,48332
	II		11,7	11,81934	0,989903	11,29328
	III		11,4	11,64059	0,979331	11,65556
	IV		12,3	11,46185	1,073125	12,44982
	I		9,03	11,28311	0,800311	10,79903
	II		10,2	11,10437	0,914055	10,61014
	III		11,7	10,92563	1,074538	10,93967
	IV		12,6	10,74689	1,16871	11,67323
	I		10,7	10,56815	1,012476	10,11474
	II			10,38941	0,962519	9,926997
	III		9,7	10,21066	0,949987	10,22379
	IV		10,2	10,03192	1,016754	10,89664
Прогноз	по тренду	средние индексы	по модели
	I		–	9,853182	0,957097	9,430449
	II		–	9,674441	0,955492	9,243853
	III		–	9,495699	1,001285	9,507905
	IV		–	9,316958	1,086197	10,12005

Подставив в это уравнение порядковые номера ряда, рассчитаем теоретические значения показателя по тренду и занесем их в следующий столбец. Поквартальные индексы сезонности найдем как отношение фактических значений уровня ряда к уровням ряда, рассчитанным по тренду. Тем самым мы заполним следующий столбец таблицы.

Чтобы рассчитать значения показателя на перспективу (прогноз), необходимо прогноз по тренду умножить на средние значения индекса сезонности. Все проведенные расчеты и исходная информация отражены на рисунке 7.8.

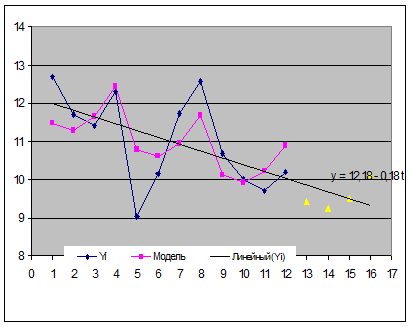
Рисунок 7.8. График результатов анализа динамики показателя с учетом тенденции и сезонных колебаний.

Из рисунка видно, что четко выраженная тенденция к уменьшению показателя накладывается на сезонные подъемы в четвертом квартале каждого года и спады в другие кварталы.

2) Уравнение в виде «гармоник ряда Фурье»:

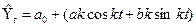(7.25)

где k определяет номер гармоник с точностью до четырёх знаков.

Под гармоникой понимают полную волну синусоиды (гармонику Фурье), где

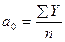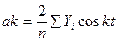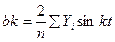; ; (7.26)

Этот метод анализа сезонных колебаний дает хорошие результаты, когда нет необходимости в четком построении уравнения тренда.

Дата добавления: 2014-01-04