В 7. Корреляция рядов динамики. Регрессия рядов динамики

Статистика в анализе рядов динамики ставит перед собой задачу совместного анализа рядов динамики, уровни которых технологически или экономически связаны друг с другом. Например, ряд уровня рентабельности связан с рядом уровня себестоимости продукции, с рядом уровня трудоёмкости и т.д. Причем изменение одного показателя вызывает изменение другого. Поэтому перед статистическим исследование “связанных” друг с другом рядов стоит проблема:

1) оценить тесноту связи между значениями уровней различных рядов;

2) построить уравнение регрессии, связывающее результативный показатель, факторный показатель и временной параметр t.

Проблема оценки тесноты связи осложняется возможным наличием автокорреляции в рядах динамики. Поскольку технологический процесс производства и реализации сельскохозяйственной продукции растянут во времени, то может оказаться, что каждый последующий уровень ряда зависит с определённой величиной лага L от предыдущих значений уровней ряда. Это явление называется автокорреляцией. Наличие автокорреляции в рядах динамики искажает результаты исследования. Поэтому разные авторы в учебной литературе предлагают несколько различных методик оценки тесноты связи и построения уравнения регрессии в рядах динамики и позволяющих исключить влияние автокорреляции.

Пусть есть два ряда с трендами: 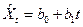(7.27)

Чтобы избежать автокорреляции или влияния автокорреляции на результаты исследований, некоторые авторы предлагают проводить анализ не уровней ряда, а их отклонений от теоретических значений по тренду, если тренд существует, или от средних значений, если отсутствует тренд и колебания показателей случайны:

 или 

или 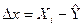(7.28)

Составляется таблица для расчета парного коэффициента корреляции на основании значений абсолютных отклонений:

Таблица 7.13. Схема расчетов для оценки тесноты связи факторов

Период	Δx	Δy	Δx Δy	Δ^²x	Δ^²y
...	...	...	...	...	...
...	...	...	...	...	...
Итого	åΔx	åΔy	åΔx yΔ	åΔ²x	åΔ^²y

Парный коэффициент корреляции факторов Х и У будет равен:

(7.29)

Дата добавления: 2014-01-04