Проверка статистических гипотез. Тема 6. Проверка статистических гипотез и оценка параметров

Тема 6. Проверка статистических гипотез и оценка параметров

План:

1. Проверка статистических гипотез

2. Критерий согласия Пирсона

3. Оценка параметров генеральной совокупности

3.1. Оценка средней арифметической генеральной совокупности

3.2. Оценка дисперсии генеральной совокупности

В спорте часто решаются вопросы:

- сравнение результатов различных групп;

- оценка точности результатов измерений;

- отыскание законов распределения изучаемых результатов;

- проверка эффективности мероприятий, направленных на совершенствование тренировочного процесса или укрепление здоровья людей, занимающихся физической культурой и спортом и т.д.

Все эти вопросы решаются с использованием приемов проверки гипотез.

Определение Статистической гипотезой называется проверяемое математическими методами предположение относительно статистических характеристик результатов измерений или относительно их закона распределения.

Обозначение: H₀- нуль-гипотеза.

Примеры:

1) H₀(D₁=D₂ ) - дисперсии результатов в первой и второй группах одинаковы, то есть значимо не отличаются.

2) H₀: результаты бега на 100м в данной группе распределены нормально.

3)H₀ () - средние результаты в контрольной и экспериментальной группах одинаковы, то есть значимо не отличаются.

При сравнении статистических характеристик (см. пример 1,3) почти никогда не встречается случая их абсолютного равенства. В силу каких-то случайных или закономерных причин значения их отличаются друг от друга. Задача при проверки гипотез состоит в том, чтобы отличить случайные влияния от закономерных.

При проверки любой статистической гипотезы решение экспериментатора никогда не принимается с уверенностью, то есть всегда существует некоторый риск принять неправильное решение. Оценка степени этого риска и представляет собой суть проверки статистической гипотезы. Ясно, что исключить на 100% этот риск невозможно. Но экспериментатор может выбрать определенную вероятность или уровень значимости.

Определение Достаточно малую вероятность, при которой (в данной определенной задаче) событие можно считать практически невозможным, называют уровнем значимости.

Обозначение: .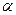

На практике обычно самыми распространенными уровнями являются: 0,1; 0,05; 0,01; 0,001.

Определение Величину q=1- 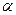называют доверительной вероятностью.

Пример: Уровень значимости 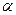=0,05, означает, что вероятность отвергнуть верную гипотезу H₀ меньше 0,05, а вероятность принять эту гипотезу равна q=1-0,05=0,95, то есть выдвинутая гипотеза принимается в 95 случаях из 100.

Как принятие, так и отклонение гипотезы осуществляется на основе определенного критерия.

Определение Статистическим критерием называется правило, обеспечивающее принятие истинной или отклонение ложной гипотезы с заранее заданной вероятностью.

Основные этапы проверки гипотезы:

1. Формулировка нуль-гипотезы.

2. Выбор уровня значимости.

3. Определение выборочного значения статистических характеристик.

4. Выбор критерия для проверки статистической гипотезы.

5. Сравнение расчетного значения с критическим значением критерия для выбранного уровня значимости и принятие или отклонение гипотезы.

Дата добавления: 2014-01-04