Теплопроводность при нестационарном режиме

7 ^2

/И —

(2.46)

е=

Рис. 2.11. Трехслойная цилиндрическая стенка

2яЛ₁1(1₁-{₂) *\

е=

/Л

а.

(2.47) (2.48)

Рассуждая также как в случае с многослойной плоской стенкой, решаем эти уравнения относительно разности температур и почленно складываем. В результате получим

Я(л

^1

п-и =

чЛ

X,

ы

1п—+— 1п—+ — 1п —

Я =

2Щ_Х -1_А)

(Ал Ял (*'> Я-з Й1

Формула (2.48) представляет собой уравнение теплопроводности для трехслойной цилиндрической стенки.

Для многослойной цилиндрической стенки, имеющей п слоев, уравнение (2.48) можно записать в виде

2тй{1_х -(_п+х)

<2 =

(2.49)

Ч+\

1п

А 1

/=1 Я.- </■•

где Я,- - коэффициент теплопроводности /-го слоя; ф, ф+] - внутренний и наружный диаметры /-го слоя.

2.2.1.5. Теплопроводность через шаровую стенку

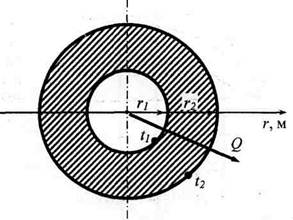Рассмотрим полый шар, внутренняя и внешняя поверхности которого имеют радиусы г\ и г2, соответственно. Источник тепла находится внутри шара. Поверхности шара поддерживаются при постоянных температурах // и /?, причем температура изменяется только в направлении радиуса (рис. 2.12).

Рассуждаем так же, как в случае однослойной цилиндрической стенки. Выделим внутри шара элементарный шаровой слой. Тепловой поток, проходящий через шаровой слой радиусом г и толщиной Ф, находим из уравнения Фурье:

(2.50)

2 = -Я^ = -Я^4лг².
йг йг

(2.51)

Разделяя переменные, получим

Рис. 2.12. Полый шар

&

4пХ

Интегрируя уравнение (2.51) по / и по г, постоянные интегрирования определяем из граничных условий: при г» г\ I- /;, а при г = г₂1 = 12-

'''■' В результате получим выражение

4пЩ-{₂) 2лгЯ(Г₂ -/₂)

а=

(2.52)

^_ ^________ 1_

Уравнение (2.52) является уравнением теплопроводности для однослойной шаровой стенки. Из этого уравнения видно, что температура в шаровом слое будет изменяться по гиперболической кривой.

т ипр-

2.2.2.1. Общие закономерности нестационарных процессов

В этом пункте рассматриваются процессы переноса теплоты за счет теплопроводности при отсутствии внутренних источников теплоты, когда температура системы изменяется не только от точки к точке, но и с течением времени. Такие процессы теплопроводности, когда поле температуры в теле изменяется не только в пространстве, но и во времени, называют нестационарными. Они имеют место при нагревании (охлаждении) различных заготовок и изделий, производстве стекла, обжиге кирпича, вулканизации резины, пуске и останове различных теплообменных устройств, энергетических агрегатов и т. д.

Среди практических задач нестационарной теплопроводности важнейшее значение имеют две группы процессов: а) тело стремится к тепловому равновесию; б) температура тела претерпевает периодические изменения.

К первой группе относятся процессы прогрева или охлаждения тел, помещенных в среду с заданным тепловым состоянием, например, прогрев болванки в печи, охлаждение металлических брусков и чушек, охлаждение закаливаемой детали и т. п.

Ко второй группе относятся процессы в периодически действующих подогревателях, например, тепловой процесс регенераторов, насадка которых то нагревается дымовым газами, то охлаждается воздухом.

На рис. 2.13 показан характер кривых, полученных при нагревании однородного твердого тела в вреде с постоянной температурой (_ое. По мере нагрева температура в каждой точке асимптотически приближается к температуре нагревающей среды. Наиболее быстро изменяется температура точек, лежащих вблизи поверхности тела (_юв. С увеличением времени прогрева эта разность будет уменьшаться, и теоретически через достаточно большой отрезок времени она будет равна нулю.

В условиях передачи теплоты через стенку при внезапном изменении температуры одного из теплоносителей не вся теплота будет передаваться через стенку: часть ее уйдет на изменение внутренней энергии самой стенки (ее температуры), и только цри наступлении стационарного процесса вся теплота будет передаваться через стенку от одной жидкости к другой.

Рис. 2.13. Характер изменения температуры тела во времени

Приведенные примеры указывают на то, что нестационарные тепловые процессы всегда связаны с изменением внутренней энергии, или энтальпии, вещества.

Передачу теплоты при нестационарном режиме можно определить, если найти закономерности изменения температурного поля и теплового потока в пространстве и во времени:

\* = 1\(х,У,г,%) Ш = /₂(х,У,г,*)'

(2.53)

Эти зависимости могут быть найдены из дифференциального уравнения теплопроводности

Дата добавления: 2014-01-04