Лекция 19. Расчёт электростатических полей

Цель лекции: изучить граничные условия и методы расчёта электростатических полей.

19.1 Граничные условия в электростатическом поле

Условия, которым удовлетворяют вектора поля на границе раздела двух различных сред, называются граничными условиями. Рассмотрим границу двух непроводящих сред, диэлект­рические проницаемости которых равны 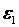и 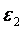. Первое граничное условие

или . (19.1)

На границе двух непроводящих сред тангенциальные составляющие вектора напряженности электрического поля равны. На поверхности раздела двух сред потенциал непрерывен .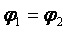

Второе граничное условие

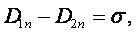(19.2)

. (19.3)

Нормальная составляющая вектора электрического смещения на границе двух непроводящих сред претерпевает скачок, равный поверхностной плотности свободных зарядов, распределен­ных на границе.

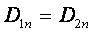Если , то , . (19.4)

Нормальная составляющая вектора электрического смещения на границе непрерывна.

Если одна из сред проводящая, то граничные условия изменятся. В проводящей среде векторы поля равны нулю, а потенциал всех точек проводника один и тот же. Пусть первая среда — диэлектрик с относительной

проницаемостью , вторая — проводник; тогда граничные условия запишутся следующим образом

,

(19.5)

.

19.2 Методы расчёта электростатических полей

Расчет электростатических полей чаще всего сво­дится к определению напряженности поля Е при заданном распределении зарядов, возбуждающих поле. Если непо­средственное определение Е приводит к математическим трудностям, удобнее вначале определить потенциал 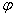по заданному распределению зарядов, а затем, зная потенциал, определить напряженность поля. Обратная задача заклю­чается в определении закона распределения зарядов по заданной напряженности поля.

Наиболее общим методом расчета полей является метод интегрирования уравнений поля. Однако в ряде случаев можно использовать частные методы, которые позволяют проще и быстрее решить поставленную задачу. К ним отно­сятся: метод наложения; метод, основанный на применении теоремы Гаусса; метод конформных преобразований; метод зеркальных изображений; графические и ряд других ме­тодов. Рассмотрим некоторые из перечисленных методов.

19.3 Метод наложения

Если распределение заряда в пространстве задано, то, разделив этот заряд на бесконечно малые элементы dQ и считая их точечными, можно определить потенциал и на­пряженность поля по формулам

, (19.6)

. (19.7)

Складывая алгебраически величины , можно опреде­лить потенциал в любой точке поля

. (19.8)

Напряженность 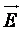определится по формуле

. (19.9)

19.4 Метод зеркальных изображений

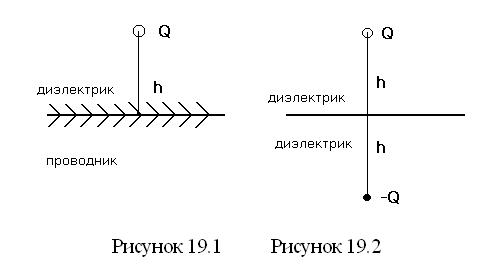
Если электрические заряды расположены вблизи гра­ницы двух разнородных сред, то векторы поля можно определить, применив искусственный метод расчета, кото­рый носит название метода зеркальных изображении.

Идея метода заключается в том, что вместо неоднородной среды рассматривается однородная среда, влияние же неод­нородности учитывается введением фиктивных зарядов. Определив векторы поля от совместного действия заданных и фиктивных зарядов, записывают граничные условия основной задачи и, пользуясь ими, находят искомые век­торы поля.

19.5 Распределение потенциалов и зарядов в системе проводящих тел

При исследовании процессов в линиях электропередач может встретиться следующая задача. Дано несколько па­раллельных проводов. Взаимное их расположение и элект­рические заряды на них известны. Требуется определить потенциалы этих проводов. Обозначим потенциал произ­вольной точки р, обусловленный заря­дом одного из проводов через. Так как потенциал и заряд пропорциональны, то

. (19.10)

Коэффициент — величина постоянная. Если число всех проводов обозначить п, то потенциал в точке р, обу­словленный зарядами всех проводов, можно определить, пользуясь принципом наложения

.(.19.11)

Если точку р выбрать на поверхности первого провода, то его потенциал

(19.12)

Аналогично можно записать потенциалы остальных про­водов

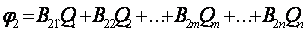
(19.13)

)

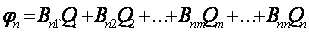Предположим, что все заряды, кроме 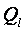, равны нулю, a 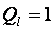. Тогда . Следовательно, коэффициент численно равен потенциалу провода k, когда заряд про­вода равен единице, а заряды остальных проводов равны нулю. Постоянные В называются потенциальными коэффи­циентами. Они всегда положительные. При перестановке индексов коэффициент не изменяется: . Если по­лученную систему уравнений решить относительно зарядов, то

. (19.14)

Постоянные А называются емкостными коэффициен­тами. Связь между потенциальными и емкостными коэффи­циентами следующая

, (19.15)

где определитель системы

, (19.16)

а алгебраическое дополнение:

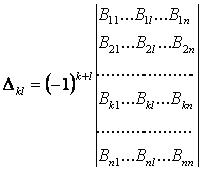
. (19.17)

Коэффициенты А с одинаковыми индексами положи­тельны, с различными индексами — отрицательны. При перестановке индексов коэффициент не меняется . Пусть потенциал одного из проводов, например 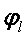, равен единице, а потенциал остальных проводов равен нулю. Тогда .

Следовательно, коэффициент 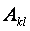численно равен за­ряду 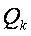,когда потенциал, а потенциал остальных проводов равен нулю.

Систему уравнений можно записать иначе

где . (19.18)

Коэффициенты С называются частичными емкостями. Если индексы у частичной емкости одинаковые, ее назы­вают собственной частичной емкостью, если индексы раз­ные — взаимной частичной емкостью. Частичные емкости всегда положительные. При изменении порядка индексов коэффициент не ме­няется .

Коэффициенты А могут быть определены эксперимен­тально. Зная их, можно подсчитать частичные емкости.

Дата добавления: 2014-01-04