Сила давления вагона на рельсы

Определим силы давления на рельсы передних и задних колес (передней и задней вагонных тележек) вагона, стоящего на горизонтальном участке пути. Масса вагона m. Пусть центр тяжести вагона из-за неравномерной загрузки расположен на некотором расстоянии l от передней оси. Расстояние между осями вагона L (рис. 6.3). На вагон с грузом действуют со стороны Земли силы тяжести вагона m g и рельсы. Рельсы действуют в точках контакта с передними и задними колесами с силами нормального давления N_п и N_з.

Мысленно уберем рельсы. Вагон, висящий в пространстве под действием всех указанных сил, должен оставаться в равновесии. Он не должен ни перемещаться поступательно, ни вращаться. Запишем для вагона условие отсутствия поступательного движения: сумма проекций сил на вертикальную ось координат OY равна нулю:

N_п +N_з – m g = 0. (6.4)

В этом уравнении две неизвестные силы N_п и N₃ – силы нормального давления рельсов на передние и задние колеса. Поэтому необходимо еще одно уравнение равновесия – условие отсутствия вращения. Как видно на рис. 6.4 силы, действующие на вагон, не сходятся в одной точке и, следовательно, создают вращающий момент сил. Видимой оси вращения нет на рисунке. Но это не важно. Где бы ни расположить возможную ось вращения, перпендикулярную плоскости рисунка, все равно сумма моментов сил для неподвижного вагона должна быть равна нулю. Выгодно ось вращения выбрать проходящей через точки опоры либо передних, либо задних колес. В этом случае плечи сил давления N_п или N_з будут равны нулю. Пусть ось проходит через точки опоры передних колес П. Моменты силы тяжести mg l действует относительно оси П против часовой стрелки. Будем считать его отрицательным. А момент силы давления рельсов на задние колеса N_зL – по движению часовой стрелки – положительным. В итоге уравнение равновесия, то есть равенство нулю суммы моментов сил относительно оси П, будет

− m g l + N₃ L = 0. (6.5)

Отсюда сила давления на задние колеса равна .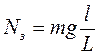

Подставив N₃ в уравнение (6.5) или записав уравнение моментов сил относительно оси задней оси, получим .

Чем ближе к оси расположен центр тяжести, тем больше сила давления рельсов на эту колесную пару. Сила давления на передние и задние колеса будет одинакова и равна половине силы тяжести вагона, если центр масс находится посередине.

Рассмотрим режим ускоренного движения вагона. Очевидно, силы давления на колеса вагона со стороны рельсов N_п и N_з отличаются от полученных для неподвижного вагона. Выделим мысленно вагон из состава (рис. 6.4). Вагон покоится относительно поезда, но поезд является неинерциальной системой отсчета. Поэтому для соблюдения равновесия следует ввести силу инерции: . Сила инерции приложена к центру масс вагона и направлена против вектора ускорения.

Пусть центр масс вагона находится на расстоянии l от передней оси. Со стороны передней и задней частей состава на автосцепки вагона действуют силы натяжения F_п и F_з. При движении со стороны рельсов действует сила сопротивления качению колес: F_сопр=μ_сопрmg. Под действием указанных сил вагон должен оставаться в равновесии относительно поезда. Запишем уравнение равновесия вагона в проекции на ось Ох

Ох: –F_ин+ (F_п– F_з) – F_сопр = 0. (6.6)

Запишем уравнения равновесия вагона под действием моментов сил относительно осей, проходящих через точки контакта передних и задних колес

–mgl+ N_з L+ (F_п –F_з) h – F_инH = 0, (6.7)

mg (L–l) – N_п L+ (F_п – F_з) h – F_инH = 0. (6.8)

Подставим из уравнения (6.6) разность сил натяжения. Тогда силы давления рельсов на передние и задние колеса вагона будут равны

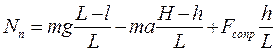, . (6.9)

Если сопоставить с результатами расчета для неподвижного вагона, то при движении с ускорением сила инерции разгружает передние колеса и нагружает задние колеса. А сила сопротивления – наоборот. Как и должно быть, сумма сил давления, несмотря на перераспределение их величин, равна силе тяжести вагона.

Дата добавления: 2014-01-04