Закон сохранения импульса

Задачи

1. Определить силу сжатия автосцепок первого и последнего вагонов состава, стоящего на спуске дороги с уклоном 0,005. Масса состава 2000 т, масса вагона 40 т. Тормозные башмаки под последним снизу вагоном.

2. Определить горизонтальную силу, достаточную, чтобы стронуть четырехосный вагон с места, если перед колесом ступенька высотой 3 1мм. Радиус колеса 0,51м. Масса вагона 20 т.

3. При наезде на препятствие последний вагон массой 60 т опрокинулся относительно передней тележки. Определить ускорение при торможении состава, если центр тяжести вагона на высоте 2 м посередине вагона, расстояние между осями крайних колес 15 м.

4. Опрокинется ли на повороте радиусом 600 м вагон массой 20 т силами давления 550 кН и 600 кН соседних вагонов. Расстояние между автосцепками 18 м. Центр масс вагона на высоте 1,8 м посередине, высота автосцепок 1,3 м.

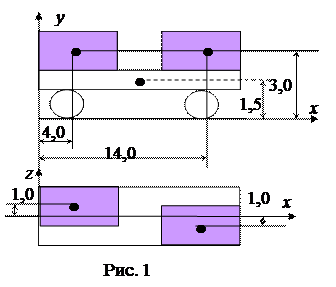
5. Определить координаты центра масс вагона, нагруженного двумя контейнерами массой по 10 т и 18 т. Масса порожнего вагона 30 т, длина 18 м. Числа на рис. 1 – расстояния в метрах до центров масс контейнеров и вагона.

6. Определить силы давления трех труб массой по 3 т на стенки и пол вагона, если ширина вагона 3,0 м, диаметр труб 1,26 м.

7. Какой вращающий момент сил должен создать тяговый двигатель, чтобы стронуть с места моторный вагон массой 20 т. Передаточное отношение равно 3,5. Радиус колеса 0,51 м, коэффициент сопротивления 0,005.

7. ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ

Три закона Ньютона являются важнейшими законами природы и позволяют решать любые задачи механики, достаточно только знать закономерности сил. Однако, если проинтегрировать уравнение второго закона Ньютона по времени взаимодействия тел, то можно прийти к понятию импульса, и если проинтегрировать по перемещению, то прийти к понятию энергии. Оказывается, что для замкнутых систем тел интегралы движения (импульс и энергия) обладают способностью сохраняться. Теперь даже не зная закономерностей для сил взаимодействия, используя законы сохранения, можно рассчитать параметры движения в процессе взаимодействия тел. Законы сохранения являются фундаментальными законами природы.

Рассмотрим систему, состоящую из нескольких тел N. Запишем для некоторого тела уравнение второго закона Ньютона: изменение импульса тела равно импульсу силы, действующей на тело

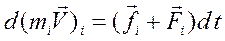. (7.1)

……………………………………………….

…………………………………………….

Здесь f_i – равнодействующая всех внутренних сил. действующих на это тело со стороны других тел системы и F_i – равнодействующая сил со стороны внешних тел, не входящих в рассматриваемую систему. Индекс i – номер тела системы. Сложим все уравнения:

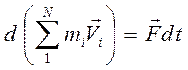. (7.2)

Здесь 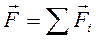– сумма внешних сил. Внутренние силы, действующие попарно, сократились.

Рассмотрим замкнутую систему тел. Система тел называется замкнутой, если внешние силы или отсутствуют или взаимно компенсируют друг друга. Для замкнутой системы тел правая часть уравнения второго закона Ньютона для системы тел (7.2) равна нулю. То есть изменение суммы импульсов тел системы равно нулю, но это значит, что сама сумма импульсов тел постоянна. Отсюда следует один из важнейших законов природы – закон сохранения импульса: в замкнутой системе тел векторная сумма импульсов тел постоянна. Или иначе: в замкнутой системе тел сумма импульсов тел в начале процесса взаимодействия равна сумме импульсов тел после окончания процесса

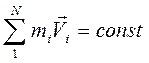или 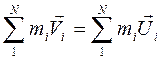. (7.3)

Возможна ситуация, когда на какую либо координатную ось проекция векторной суммы внешних сил, действующая на систему тел, равна нулю. В этом случае, хотя импульс системы в целом не сохраняется, но сохраняется проекция импульса системы тел на эту ось.

Получим важное следствие закона сохранения импульса. Известно, что радиус-вектор центра масс системы из N тел определяется выражением 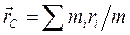. Здесь m_i и r_i – масса и радиус-вектор тела с номером i, m – масса системы тел. Продифференцируем по времени это выражение с учетом, что производная от радиус-вектора некоторого тела по времени это скорость тела. В результате получим 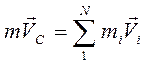. Отсюда следует: сумма импульсов тел равна произведению массы системы на скорость центра масс. Произведя замену в уравнении (7.2), получим уравнение второго закона Ньютона для движения центра масс

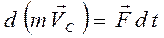. (7.4)

Центр масс системы тел движется как материальная точка, в которой сосредоточена вся масса системы тел, под действием результирующей внешней силы.

Для замкнутой системы тел внешние силы или отсутствует, или скомпенсированы. Тогда центр масс движется в пространстве прямолинейно и равномерно. А если в начальный момент времени центр масс покоился, то его координаты будут постоянны, какие бы сложные движения не совершали отдельные тела системы.

Дата добавления: 2014-01-04