Пружинный маятник

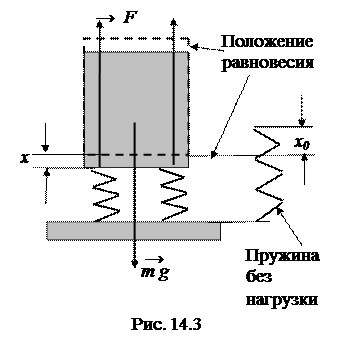
Рассмотрим колебания пружинного маятника на примере вертикальных колебаний вагона. Пусть вагон, опирающийся на пружины подвески, выведен из положения равновесия в вертикальномнаправлении и отпущен. Под действием сил упругости он начнет смещаться обратно к положению равновесия, увеличивая скорость движения. В положении равновесия он не остановится, а по инерции продолжит движение, пока сила упругости не остановит его. Потом движение под действием упругой силы повторится в обратном направлении, и возникнут собственные колебания вагона.

x

Когда вагон находится в равновесии, то сила тяжести вагона компенсируется силой упругости пружин mg = kx ₀ (рис. 14.3). Здесь
х ₀ – деформация первоначально свободных пружин под действием силы тяжести вагона, – суммарный коэффициент упругости всех пружин подвески, соединенных параллельно. При смещении вагона в процессе колебаний относительно положения равновесия на расстояние х результирующая сила, действующая на вагон, будет равна F = – k (x ₀ +x) + mg = – k x. То есть сила тяжести вагона, скомпенсированная силой упругости предварительного сжатия пружин, на процесс колебаний не влияет.

Определим период свободных колебаний кузова вагона. Запишем уравнение второго закона Ньютона для смещения вагона под действием возвращающей силы упругости пружин подвески F= – kx

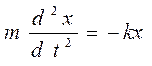. (14.6)

Здесь ускорение записано как вторая производная от координаты по времени. Уравнение (14.4) – это дифференциальное уравнение второго порядка. Решением уравнения является функция, превращающая его в тождество. То есть эта функция и ее вторая производная должны иметь одинаковую зависимость от времени, но разного знака. В математике такими функциями являются функция синуса и косинуса и экспонента с мнимым показателем.

Ищем решение в виде гармонической функции x = A cos ωt. Вторая производная функции равна 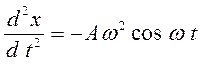. Подставив искомое решение в дифференциальное уравнение второго закона Ньютона, убедимся, что оно превращается в тождество при условии, если циклическая частота колебаний равна 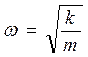. Соответственно, период вертикальных свободных колебаний будет равен

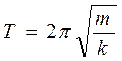. (14.7)

Период свободных вертикальных колебаний не зависит от амплитуды колебаний вагона. Период возрастает при увеличении массы вагона (например, при погрузке) и при уменьшении упругости пружин. Для пассажирских вагонов, с целью обеспечения комфорта пассажирам, упругость пружин подвески выбирается, сравнительно с грузовыми вагонами, небольшой, так чтобы частота собственных колебаний была бы около 2 Гц, при которой пассажир испытывает сонливость.

Амплитуда свободных колебаний А определяется энергией Е, сообщенной внешним воздействиям в начале при возбуждении колебаний. Энергия колебаний равна максимальному значению потенциальной энергии 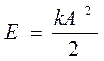. Откуда амплитуда колебаний равна

. (14.8)

При вертикальных колебаниях вагона сила давления колес на рельсы из постоянной, равной силе тяжести вагона, превратится в пульсирующую по величине силу. Добавочная сила будет равна силе инерции F=ma или равной ей силе упругости пружин подвески F=kx,

. (14.9)

Периодическая нагрузка на колеса, рельсы, кузов вагона отрицательно влияет на вагоны, выводит их из строя раньше, чем постоянное воздействие даже большей величины силы. Колебания ухудшают сцепление колеса с рельсом. В момент минимального давления, может происходить частичное буксование, сход колеса с рельса. Поэтому возникшие колебания следует гасить с помощью амортизаторов.

Дата добавления: 2014-01-04