Такое состояние p-n перехода называется равновесным

Суммарная протяжённость p-n перехода, в обе стороны от границы раздела, называется шириной p-n перехода l ₀. l ₀ = l _p + l _n, где l _p и l _n – ширина p-n перехода, соответственно в p и n областях.

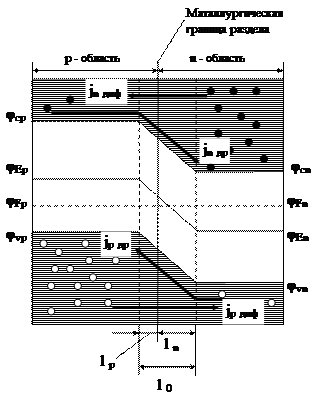Выясним, чем определяется ширина p-n перехода и протяжённость её участков l _n и l _p в n и p областях. Для этого рассмотрим зонную диаграмму контакта двух полупроводников.

Здесь мы перешли от энергетической зонной диаграммы к потенциальной зонной диаграмме имея ввиду, что φ = W/q. Так удобнее для дальнейшего рассмотрения процессов, происходящих в p-n переходе при подключении к нему внешнего источника напряжения.

Так как уровень Ферми по определению не может быть разным в n и p полупроводниках, валентные зоны и зоны проводимости в них оказываются на разных потенциальных уровнях. Следовательно середины запрещённых зон в n и p областях смещены

относительно друг друга на величину

φ_{к 0} = φ_Ep – φ_En

Эта величина называется контактной разностью потенциалов p-n перехода или его потенциальным барьером в равновесном состоянии.

Ранее были приведены выражения: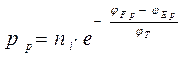 и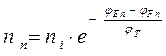

Разрешив их относительно φ_Ep и φ_En и учитывая, что n_n · p_n = n_i², в общем случае получим: .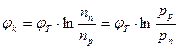

Отсюда следует, что контактная разность потенциалов p-n перехода определяется отношением концентраций одноимённых носителей заряда в смежных областях, т.е. отношением концентрации основных носителей заряда одной области к концентрации неосновных носителей заряда другой области.

В частности, для равновесного состояния: .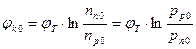

Типичная величина потенциального барьера, при температуре близкой к комнатной, составляет для германиевого перехода 0,35 – 0,4В, а для кремниевого 0,65 – 0,7В.

Электрическое поле в p-n переходе определяется на основании уравнения Пуассона:

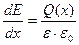, где ε – диэлектрическая проницаемость среды, а ε₀ – вакуума.

олагая, что примеси распределены в основных полупроводниках равномерно можно считать, что:

Q_p(x) = -q·N_а; -l _p ≤ x ≤0, для p – области

и Q_д(x) = +q·N_д; 0 ≤ x ≤ l _n, для n – области.

Тогда интегрируя уравнение Пуассона в соответствующих пределах, получим:

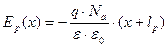и 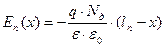. При других значениях x E = 0.

Приравнивая E _p(0) и E _n(0), получим: .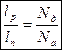

Следовательно, протяжённость объёмного заряда от границы раздела вглубь полупроводника, обратно пропорциональна степени его легирования. Объёмные заряды по обе стороны границы раздела должны уравновешивать друг друга.

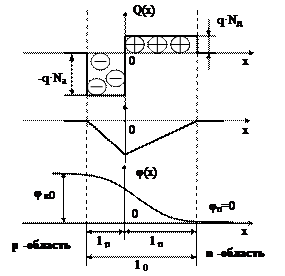По определению, напряженность поля E(x) = - dφ(x)/dx, тогда интегрируя эти выражения для

E _p (x) и E _n (x), можно определить закон изменения потенциала в p – n переходе.

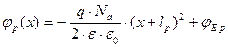и

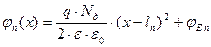
Зависимости Q(x), E(x) и φ(x) приведены на рисунке.

Приравнивая φ_n(0) и φ_p(0) и учитывая, что

φ_{к 0} = φ_Ep – φ_En найдём протяжённость областей объёмных зарядов в p – области и n – области, а также суммарную ширину p – n перехода.

, ,

.

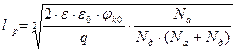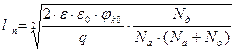Если l_n = l _p переход называется симметричным, а при l_n < l _p или l_n > l _p несимметричным.

Симметричные переходы получаются при N_а = N_д, в противном случае они несимметричные.

Если контакт полупроводников идеальный, как это определялось выше, и, к тому же, ширина p-n перехода пренебрежимо мала по сравнению с линейными размерами его площади, то такой p-n переход считается близким к идеальному.

Рассмотренный нами p-n переход относится к так называемым ступенчатым или резким переходам из-за резкого характера изменения концентрации примесей одного элемента на другой. Плавными называют переходы в которых переход на границе раздела от примеси одного элемента к другой примеси происходит плавно.

Современные технологии и оборудование позволяют получать p-n переходы близкие к резкому, поэтому при дальнейшем изучении процессов, происходящих в p-n переходах, будем считать их резкими.

3.2. Воздействие внешнего источника напряжения на состояние p – n перехода.

3.2.1. Обратное смещение p-n перехода.

Рассмотренное выше состояние термодинамического равновесия можно нарушить, приложив к p-n переходу с помощью внешнего источника, напряжение в той или иной полярности. Для этого на внешних торцах полупроводников специальной технологией, препятствующей образованию ненужных в данном случае дополнительных p-n переходов, выполняются омические контакты.

Для начала будем считать, что омические контакты и области полупроводников за пределами объёмного заряда имеют пренебрежимо малую величину сопротивления по отношению к сопротивлению области объёмного заряда. При этих условиях, независимо от величины токов, протекающих по цепи, поле E_вн, создаваемое внешним источником, будет полностью сосредоточено 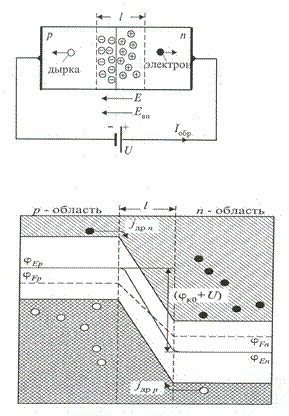внутри p-n перехода. В зависимости от полярности подключения, это поле будет или вычитаться или складываться, с полем объёмного заряда. Если приложить к p-n переходу внешнее напряжение, в полярности, указанной на рисунке, то дырки p-области будут оттягиваться к отрицательному полюсу источника, а электроны n-области к положительному полюсу. При этом происходит оголение более глубинных слоёв ионов примесей в обоих полупроводниках, следовательно растёт объёмный заряд и напряжённость создаваемого им электрического поля.

Как видно по зонной диаграмме, потенциальный барьер, равный в равновесном состоянии φ_к0 , возрастает на величину приложенного внешнего напряжения U т.е. φ_к = φ_{к 0} + U.

Такое смещение p-n перехода называется обратным. Очевидно, что это приводит к уменьшению диффузионной составляющей тока через p-n переход и увеличению дрейфового тока. Баланс токов нарушается и в цепи протекает дрейфовый ток неосновных носителей заряда или т.н. обратный ток I _обр. При возрастании обратного напряжения от 0 приблизительно до 0,1В обратный ток I _обр = I _диф – I _др будет увеличиваться за счёт уменьшения диффузионной составляющей. При напряжениях больших 0,1В можно считать I _диф = 0, и через переход будет идти только дрейфовая компонента тока которая для идеального перехода не зависит от приложенного напряжения. Поэтому её часто называют током насыщения перехода и обозначают I ₀. Величина I ₀ очень мала т.к. она обусловлена потоком неосновных носителей концентрация которых в высоколегированных полупроводниках незначительна.

3.2.2. Прямое смещение p-n перехода.

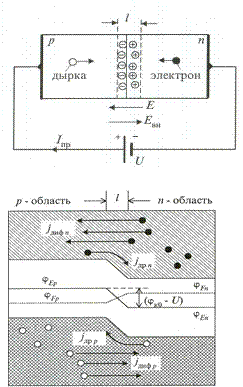Изменим полярность подключения внешнего источника на противоположную, как показано на рисунке. При этом основные носители заряда будут подтягиваться к области объёмного заряда, частично компенсируя его в зависимости от приложенного напряжения. Это приведёт к уменьшению объёмного заряда в переходе, а следовательно к снижению потенциального барьера, высота которого будет равна φ_к = φ_{к 0} - U.

Поэтому большее число основных носителей заряда,

обладающих достаточной энергией, будут в состоянии преодолеть потенциальный барьер и перейти в смежную область. Диффузионный ток увеличится по сравнению с равновесным значением, а дрейфовая составляющая не меняется, т.к. для неосновных носителей поле объёмного заряда по прежнему является ускоряющим. По мере увеличения напряжения диффузионный ток растёт и может достигать весьма больших значений, т.к. он обусловлен током основных носителей, концентрация которых, при высокой степени легирования может быть весьма большой. Такое смещение p-n перехода называется прямым, а соответствующий ему ток – прямым током p-n перехода.

Отношение прямого тока к обратному может иметь значения порядка 10 ³ ÷10 ⁶.

Это позволяет говорить об односторенней проводимости p-n перехода.

Ширина p-n перехода, при смещении его постоянным напряжением, определяется из его выражения для равновесного значения, подстановкой вместо φ_к0 значения φ_к = φ_к0 – U.

.

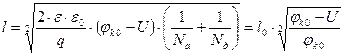Отсюда видно, что ширина перехода сужается при прямом смещении U >0 и расширяется при обратном смещении U <0.

3.3. Граничные концентрации неравновесных неосновных носителей заряда.

3.3.1. Инжекция и экстракция носителей заряда.

Смещение p-n перехода приводит к изменению граничных концентраций неосновных носителей заряда по обе его стороны. Под граничной концентрацией носителей имеется ввиду их концентрация на границе объёмного заряда с основной p или n – областью.

Потенцируя полученное ранее выражение 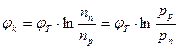для контактной разности потенциалов, в общем случае для неравновесного состояния, можем записать:

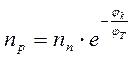и 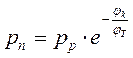, а для равновесного состояния:

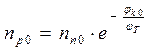и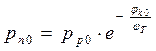

Тогда: 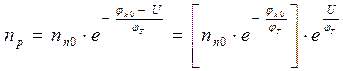. Сомножитель в квадратных скобках

есть n _p0, поэтому: 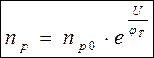. Аналогично, для p_n получим:

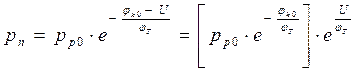, или .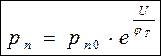

Из этих выражений для перехода в неравновесном состоянии следует, что при прямом смещении U>0 происходит увеличение концентрации неравновесных носителей на границах перехода по сравнению с равновесными значениями т.е. n_p > n_p0, и p_n > p_n0. Такое принудительное введение избыточных носителей (впрыскивание) носит название инжекции. При обратном смещении U<0 происходит уменьшение граничных концентраций по сравнению с равновесной т.е n_p < n_p0, и p_n < p_n0. Такой принудительный отбор (выкачивание) носителей называется экстракцией. Величины избыточных граничных концентраций Δ n_p и Δ p_n можно получить вычитая равновесные концентрации из неравновесных:

.

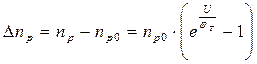
Поделив эти выражения, получим: .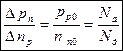

В симметричных переходах инжекция носит двусторонний характер, а в несимметричных - преимущественно односторонний. В этом случае, область с высокой степенью легирования, т.е. более низкоомную, называют эмиттером, а высокоомную, с меньшей степенью легирования - базой.

3.4. Вольтамперная характеристика идеального p-n перехода.

Дата добавления: 2014-01-04