Уравнение непрерывности заряда является выражением общего закона неопределённости в физике

Его физический смысл состоит в том, что заряды в некоторой области не могут возникать или исчезать за бесконечно короткие промежутки времени, т.к. на это требуется бесконечно большая энергия.

Применительно к решаемой нами задаче, для идеализированного перехода уравнение непрерывности приводится к следующим выражениям, которые называются уравнениями диффузии: .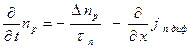

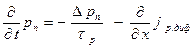Для количественного определения токов через p – n переход уравнения диффузии для электронов и дырок соответственно, решаются совместно с приведёнными ранее уравнениями плотности токов. j_{n диф.} = q·D_n·∂ n_p/∂x, j_{p диф.} = -q·D_p·∂ p_n/∂x, где: D_n и D_p – коэффициенты диффузии, Δ n_p и Δ p_n – граничные концентрации, τ_n и τ_p – время жизни электронов и дырок соответственно, т.е. время, в течение которого концентрация соответствующих носителей заряда уменьшается в е ра з, x – расстояние, отсчитываемое от границы p-n перехода вглубь области электронного или дырочного полупроводника.

Окончательное решение этих уравнений имеет вид:

для x>0,

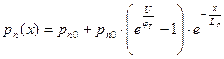
для x <0.

,

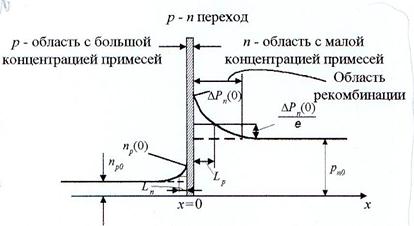
Здесь: L_n и L_p – диффузионная длина электронов и дырок соответственно, т.е. расстояние, на котором соответствующая концентрация в результате рекомбинации убывает в e раз по сравнению с её граничным значением Δn(x) или Δp(x).

Диффузионная длина, время жизни и коэффициенты диффузии связаны соотношениям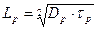и:

и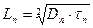

Подставляя выражения для концентраций в уравнения плотности токов, получим:

, .

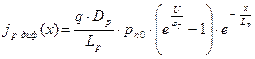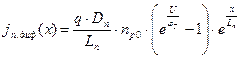Хотя, как следует из этих выражений, j_{n диф} и j_{p диф} зависят от x, общий ток p-n перехода постоянен в любом сечении полупроводника. Вблизи границ перехода, при x=0, этот ток практически диффузионный, поэтому он может быть найден как сумма j _диф = j_{n диф} + j_{p диф} при x=0.

.

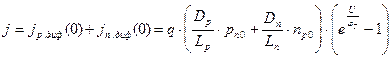Соответственно, ток I через p-n переход площадью S равен I = j · S.

Подставив в эту формулу найденное значение плотности тока, получим:

.

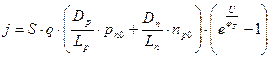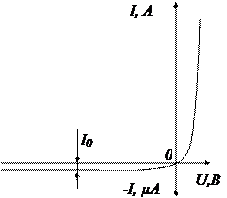Как это следует из выражения, ток I через p-n переход является экспоненциальной функцией приложенного к нему напряжения U и температуры T (φ_T = k·T/q). Кроме того, при U = const, величина тока определяется параметрами S, D_n, D_p, L_n, L_p, p_n0, n_p0, характеризующими геометрию перехода, материал полупроводников, концентрацию неосновных носителей, а значит концентрацию примесей (степень легирования). Поэтому коэффициент при экспоненте удобно выделить, обозначив его как I ₀.

.

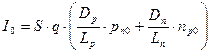Тогда ток I через p-n переход .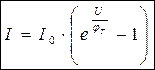

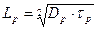Статическая вольтамперная характеристика p-n перехода

Проанализируем выражение для тока I ₀. Учитывая, что и 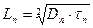получим:

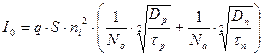. Поскольку, 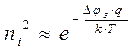где Δφ_з – ширина запрещённой зоны, то 1) - этот ток будет сильно зависеть от температуры, поэтому его часто называют тепловым. 2) – этот ток будет тем меньше, чем больше ширина запрещённой зоны Δφ_з.

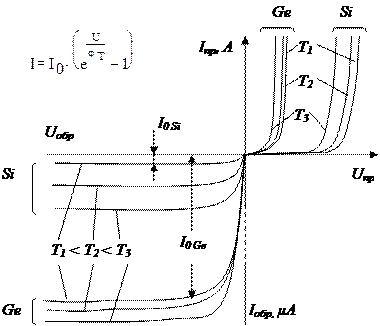Например, у кремния ширина запрещённой зоны Δφ_з = 1,12В, а у германия Δφ_з = 0,66В. Поэтому абсолютное значение теплового тока кремниевого перехода на несколько порядков меньше соответствующего тока германиевого перехода. Однако, по той же причине, относительное изменение теплового тока кремниевого перехода значительно больше чем у германиевого. В этом можно убедиться взяв производную d n _i /d T.

На рисунке дано качественное сравнение вольтамперных характеристик германиевого и кремниевого переходов, при различных температурах. Прямая ветвь вольтамперной характеристики кремниевого перехода как бы сдвинута вправо (обычно на 0,3 – 0,4В) относительно ВАХ германиевого перехода, т.к. величина I ₀, входящая масштабным множителем в выражение для тока, у кремниевых переходов на несколько порядков меньше, чем у германиевых. По той же причине обратный ток в кремниевом переходе на несколько порядков меньше, чем у германиевого. Как прямой, так и обратный токи p-n перехода возрастают с увеличением температуры, причём относительное изменение тока у кремниевого перехода выражено сильнее.

3.5. Вольтмперная характеристика реального p-n перехода.

Вольтамперная характеристика реального диода отличается от теоретической ВАХ идеализированного перехода. Расхождение в обратных ветвях связано, во-первых наличием поверхностного тока утечки I_ут, который растёт пропорционально обратному напряжению. Во-вторых, величина обратного тока в реальном переходе увеличивается за счёт термотока I_T, обусловленного процессом генерации носителей заряда в самом p-n переходе, который не учитывался при выводе ВАХ. С ростом обратного напряжения термоток растёт пропорционально .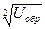

На ход прямой ветви оказывает влияние сопротивление объёмов полупроводников по обе стороны p-n перехода, которым мы пренебрегли. Особенно сильное влияние оказывает область базы, т.е. область с меньшей степенью легирования. Прямой ток создаёт на базе падение напряжения U_б = I · r_б. Поэтому напряжение, действующее непосредственно на переходе будет U - I · r_б.

3.6. Характеристические сопротивления p-n перехода.

Свойства p-n перехода количественно можно охарактеризовать его сопротивлением постоянному и переменному току. Соответственно R ₀ = U / I – сопротивление постоянному току, а R _д = dU / dI – дифференциальное сопротивление или сопротивление переменному току достаточно малой амплитуды. Вследствие нелинейности ВАХ перехода, R ₀ и R _д имеют значительно меньшие значения на прямой ветви чем на обратной. С другой стороны всегда R ₀ > R _д в области прямых токов, а в области обратных токов R ₀ < R _д. Отметим, что обе эти величины являются функциями напряжения или тока R ₀ = f(U) или R ₀ = f(I) и R _д = f (U) или R _д = f (I), т.е. значения этих величин зависят от положения точки на ВАХ в которой они были определены.

3.7. Емкостные свойства p-n перехода.

Так как процессы, происходящие в p-n переходе при изменении напряжения на нём, связаны с перемещением и изменением зарядов, следует ожидать проявления емкостных свойств перехода в целом. Различают два типа емкостных характеристик, присущих p-n переходу.

3.7.1. Барьерная или зарядная емкость p-n перехода.

Так как область объёмного заряда в переходе, представляет собой двойной слой противоположных по знаку неподвижных зарядов, а толща полупроводника по обе стороны перехода обладает достаточно хорошей проводимостью, то в целом такой p-n переход можно представить как плоский конденсатор, ёмкость которого рассчитывается по формуле

C_бар = dQ/dU = ε·ε₀·S / l.

Поскольку ширина перехода зависит от приложенного напряжения U, то и емкость будет зависеть от напряжения U.

Для ступенчатого переход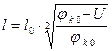а , а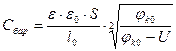

3.7.2. Диффузионная ёмкость p-n перехода.

При прямом смещении перехода в p и n областях за счёт инжекции происходит накопление подвижных неравновесных носителей заряда. Отношение изменения инжектированного заряда к изменению напряжения на переходе определяет диффузионную ёмкость p-n перехода

C_диф = dQ_инж / dU. С учётом инжекции в обе стороны p-n перехода

С_диф = q(I _p· τ_p + I _n· τ_n) / k·T,

где I_n и I_p – электронная и дырочная составляющие прямого тока. Отсюда следует, что диффузионная ёмкость пропорциональна прямому току и может достигать больших значений. Полная ёмкость p-n перехода C_пер= С_бар + С_диф.

Наличие емкости приводит к нежелательным фазовым сдвигам между напряжением на p-n перехо де и током, протекающим через него, при работе приборов на переменном токе.

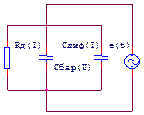
Эквивалентную схему p-n перехода при работе на малых значениях токов и напряжений можно представить в след. виде. Заметим, что параметры эквивалентной схемы зависят от постоянного смещения

на переходе. Наличие емкостей ухудшает выпрямительные свойства перехода с ростом частоты переменного напряжения.

Однако именно благодаря наличию зависимой от напряжения барьерной емкости перехода, появилась возможность создания специальных приборов, которые мы рассмотрим чуть позже.

3.8. Пробой p-n перехода. Виды пробоя переходов.

Дата добавления: 2014-01-04