
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математичні моделі САК. Рівняння динаміки і статики
|
|
|
|
МАТЕМАТИЧНИЙ ОПИС САК
На певному етапі аналізу та синтезу САК отримують її математичний опис за допомогою рівнянь (аналітичний опис), графіків, структурних схем, графів (графічний опис), таблиць (табличний опис). Причому, для опису всієї системи в цілому спочатку звичайно складають опис її окремих елементів. Так, для отримання рівнянь системи складають рівняння для кожного її елемента. Сукупність цих рівнянь називають математичною моделлю САК.
Математична модель має бути досить простою, щоб не обтяжувати дослідження, але з іншого боку – точною, щоб повніше відображати властивості самої системи.
По своїй природі САК – динамічна система і поведінка її описується диференціальними рівняннями, складеними на основі фізичних законів, що визначають поведінку системи (закон збереження матерії, енергії, другий закон Ньютона, закони Кірхгофа і т.д.).
Розв’язуючи ці рівняння, можна визначити значення вихідної величини y(t) системи в будь-який момент часу при вибраному законі зміни задавальних x(t) та збурюючих f(t) впливів.
У більшості випадків безперервні САК описуються нелінійними диференціальними рівняннями n-го порядку, які можуть бути записані у вигляді:
 .
.
Це рівняння (для спрощення припустимо, що збурюючий вплив f(t) відсутній) описує процеси в системі при будь-яких вхідних впливах і називається рівнянням динаміки.
Якщо припустити, що вплив x(t) не змінюється і має постійне значення х0, а процес у системі усталився, і вихідна координата набула значення у0, то рівняння набуде вигляду:
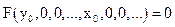 .
.
Це рівняння описує статичний режим роботи САК і називається рівнянням статики.
Статичний режим можна описати графічно за допомогою статичних характеристик. Статичною характеристикою називається залежність вихідної величини від вхідної в усталеному режимі.
У більшості випадків статичні характеристики реальних елементів нелінійні і задаються у вигляді графіків.
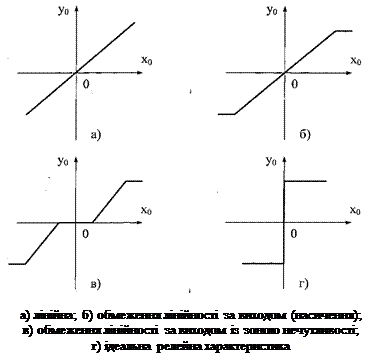 Але в ряді випадків нелінійності елементів САК є неістотними, або система працює на обмежених ділянках статичних характеристик її елементів, де нелінійність недостатньо виражена. У цих випадках реальну нелінійну характеристику вдається з певним ступенем точності замінити лінійною і здійснити лінеаризацію рівнянь, тобто замінити точні нелінійні рівняння наближеними лінійними. Це дозволяє спростити методи аналізу та синтезу САК.
Але в ряді випадків нелінійності елементів САК є неістотними, або система працює на обмежених ділянках статичних характеристик її елементів, де нелінійність недостатньо виражена. У цих випадках реальну нелінійну характеристику вдається з певним ступенем точності замінити лінійною і здійснити лінеаризацію рівнянь, тобто замінити точні нелінійні рівняння наближеними лінійними. Це дозволяє спростити методи аналізу та синтезу САК.
Якщо нелінійні статичні характеристики задані у вигляді графіків або таблиць, лінеаризацію найпростіше виконувати графічно (табличні залежності для цього необхідно також перетворити у графіки).
У результаті лінеаризації математична модель САК зводиться до системи лінійних диференціальних рівнянь чи до одного лінійного диференціального рівняння n-го порядку:
 (1)
(1)
де 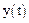 – вихідна величина елемента або системи;
– вихідна величина елемента або системи; 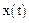 – вхідна величина елемента або системи;
– вхідна величина елемента або системи;  – коефіцієнти, які залежать від конструктивних параметрі елемента або елементів системи.
– коефіцієнти, які залежать від конструктивних параметрі елемента або елементів системи.
З метою скорочення запису, вводять оператор диференціювання
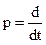 (2)
(2)
і виносять за дужки вихідну і вхідну величини, диференційне рівняння в операторній формі набуває вигляду:
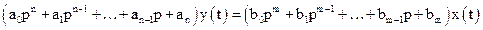 . (3)
. (3)
Представивши вираз в дужках як многочлен від 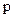 , диференціальне рівняння можна скорочено записати в наступному вигляді:
, диференціальне рівняння можна скорочено записати в наступному вигляді:
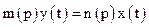 , (4)
, (4)
де
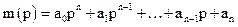 , (5)
, (5)
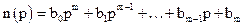 . (6)
. (6)
Вираз (5) називається вихідним оператором елемента або системи, а (6) – вхідним оператором.
Уведемо поняття передаточної функції.
Передаточною функцією в операторній формі називається відношення оператора впливу до власного оператора:
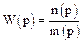 .
.
Тоді рівняння системи може бути записано в більш компактній формі:
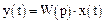 .
.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2017; Нарушение авторских прав?; Мы поможем в написании вашей работы!