Особые случаи решения транспортной задачи

Открытая модель транспортной задачи

На практике часто имеет место случай, когда

В этом случае транспортная задача называется открытой.

Чтобы решить задачу при таком условии, открытую модель превращают в закрытую. Для этого в условия задачи вводится фиктивный потребитель (или поставщик), спрос которого принимают равным разности между объемом производства и суммой спроса всех действительных потребителей.

Если обозначить спрос фиктивного потребителя через b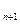, то

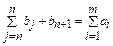
Транспортные издержки по доставке продукции фиктивному потребителю принимают равными 0, поскольку транспортировка фиктивному потребителю осуществляться не будет. Удовлетворение спроса фиктивного потребителя осуществляется в последнюю очередь. Пример открытой транспортной задачи и ее решения приведены в таблицах 15 и 16.

Таблица 15 – Открытая транспортной задачи размещения производства

Поставщики	Потребители	ui
А	Б	В	Фиктивный потребитель
450 х	360 310 150 x	440 х	250 х
	600 160 х		9) + 160	8) -
	400 250 х		10) -	8 +	0) 250
	500 50 х	5)	7)			-2
v j				-1

С₁ = 9×160 + 8×440 + 10×150 +0×250+5×450 + 7×50 = 9060

₁₁ = 8 – 7 = 1 ₁₄ = 0 + 1 = 1 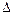₂₁ = 7 – 8 = -1

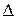₂₃ = 8 – 9 = -1 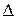₃₃= 11 – 6 = 5 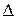₃₄ = 0 + 1 = 1

Таблица 16 – Решение открытой транспортной задачи

Поставщики	Потребители	ui
А	Б	В	Фиктивный потреби- тель
			9)	8)
				8)	0)
		5)	7)			-2
v j

С₂ = 8 910

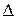₁₁ =8 – 7 = 1 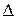₁₄ = 0 – 0 = 0 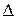₂₁ = 7 – 7 = 0

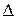₃₃ = 11 – (8 - 2) = 5 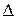₃₄ = 0 + 2 = 2 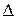₂₂ = 10 – 9 = 1

Важной особенностью транспортной задачи является то, что ее модель позволяет определить минимальные издержки не только на перевозки, но и на производство продукции вместе с доставкой ее потребителю.

Составление открытой модели с применением указанного критерия позволяет оценить перспективы предприятий, производящих однородную продукцию, в случае, если предложение превышает спрос на рынке данной продукции. Связь с фиктивным потребителем укажет на необходимость сокращения производства на предприятии.

В рассмотренной задаче на 2-м предприятии производство должно быть снижено с 400 до 150 единиц.

Вырождение при решении задач распределительным методом

Для задачи, решаемой распределительным методом, в каждой таблице необходимо выполнение следующего правила: количество заполненных клеток должно быть равно k=n+ m – 1. Это правило должно выполняться для того, чтобы на каждом шаге улучшения плана была возможность определить потенциалы и построить контур для ПОЗ.

Если же k<n+ m – 1, то вычислить некоторые потенциалы и построить некоторые контуры по общим правилам будет невозможно. Такой случай называется вырожденным. Пример вырождения приведен в таблице 17.

Таблица 17 – Случай вырождения при решении транспортной задачи

Поставщики	Потребители	ui
А	Б	В	Г
50 х	250 х	200 х	300 x
	400 х	5)
	500 450 200 х	8)	9)	8)
	300 x		3)		6)	-3
vj

В некоторых случаях вырождение можно преодолеть, если составить первоначальный план, используя другую диагональ или используя другой метод.

Если же и этот путь приведет к вырождению, то применяют следующий прием: одну из свободных клеток по строке или по столбцу заполняют условно, вписывая в нее 0 (в рассматриваемом примере это клетка (3,2)). Это итогов не искажает. При построении очередной таблицы эту клетку следует считать заполненной.

Дата добавления: 2014-01-05