Аффинные системы координат

Аффинная система координат О e1e2 … e n в аффинном пространстве A ⁿ есть совокупность, состоящая из произвольной точки О, называемой началом координат, и базиса e1, e 2 ,…, en из присоединенного линеала L.

Подчеркнем, что аффинная система координат задается двумя разнородными объектами — точкой О из аффинного пространства и базисом e1, e 2 ,…, en из присоединенного линеала.

Пусть А — произвольная точка аффинного пространства A ⁿ. Вместе с началом координат О точка А определяет элемент (радиус-вектор) r _A = OA Î Ln, координаты которого определяются из разложения по базису e 1, e 2 ,…, e n: OA = x 1e 1 + x 2e 2 +…+ xne n.

Аффинными координатами произвольной точки А Î A ⁿ называют координаты соответствующего радиус-вектора r _A = OA Î Ln и обозначают символом А (x 1, x 2 ,…, xn).

Ясно, что координаты точки А определяются однозначно в силу единственности разложения вектора по заданному базису.

Произвольный вектор AB Î Lⁿ можно представить как разность соответствующих радиус-векторов

AB = r B – r A, (3.9.1)

Если вектор AB задан координатами своего начала А (x 1, x 2 ,…, xn) и конца В (y 1, y 2 ,…, yn) относительно базиса e 1, e 2 ,…, e n, то его координаты относительно того же базиса определяются из соотношения (3.9.1) как коэффициенты разложения по указанному базису в виде

AB = (y 1 – x 1)e1 + (y 2 – x 2)e2 +…+ (yn – xn)e n

и обычно используют обозначение AB (y 1 – x 1, y 2 – x 2,…, yn – xn).

Прямой в аффинном пространстве A ⁿ, проходящей через точку C Î A ⁿ в направлении ненулевого вектора u Î Lⁿ, называется множество всех точек P Î A ⁿ, для которых CP = l u, где l Î (– ¥, ¥) — вещественное число. Указанный вектор u называется направляющим вектором прямой.

При рассмотрении аффинных систем координат в реальных пространствах: на прямой, плоскости и трехмерном пространстве, базисные векторы соответствующих линеалов V 1, V 2, V 3 приводятся в общее начало (рис. 3.9.1 – 3.9.3).

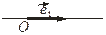Рис. 3.9.1

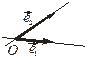Рис. 3.9.2

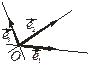Рис. 3.9.3

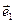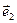Прямые в рассматриваемых пространствах, определяемые началом координат О и соответствующими базисными векторами, называются осями координат (O, O, O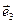 рис. 3.9.3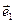; O, O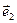 рис. 3.9.2; O 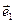рис. 3.9.1).

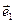
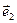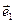
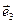В трехмерном аффинном пространстве рассматривают также координатные плоскости, определяемые соответствующими парами координатных осей (O, O, O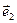 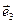рис. 3.9.3).

Определение 3.9.1. Тройка базисных векторов 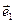, , 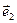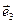называется правой (левой), если после приведения их к общему началу по этим векторам можно направить соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.

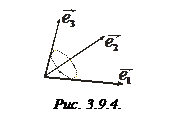Заметим, что тройка будет правой, если, находясь внутри телесного угла, образованного этими векторами, кратчайший поворот от первого из них ко второму, а затем от второго к третьему осуществляется против хода часовой стрелки (на рис. 3.9.4, например, приведена правая тройка).

Очевидно, что при круговой замене ориентация тройки не изменяется, т. е. если 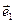, , 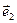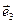правая тройка векторов, то 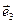, , 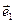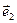и 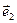, , 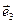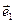также будут правыми.

Упорядоченная пара базисных векторов 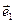, 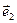называется правой (левой), если кратчайший поворот от 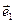к 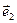происходит против (по) часовой стрелки (на рис. 3.9.2, например, приведена правая пара).

Аффинная система координат называется правой (левой), если ее базис правый (левый). В дальнейшем ради определенности будем рассматривать только правые системы координат.

Дата добавления: 2014-01-05