
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрический смысл линейной зависимости и независимости векторов на плоскости и в трехмерном пространстве
|
|
|
|
Теорема 3. 4.1. Два геометрических вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство. Необходимость. Пусть векторы  и
и  линейно зависимы, следовательно,
линейно зависимы, следовательно,  +
+ =
=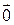 , причем хотя бы одно из чисел l 1, l 2 отлично от 0. Допустим для определенности l 2 ¹ 0. Тогда
, причем хотя бы одно из чисел l 1, l 2 отлично от 0. Допустим для определенности l 2 ¹ 0. Тогда
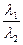
 +
+  =
= 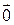 ,
,  =
= 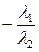
 ,
,
т. е. векторы  и
и  коллинеарны.
коллинеарны.
Достаточность. Пусть векторы  и
и  коллинеарны. Будем считать, что среди них нет нулевого вектора, ибо в противном случае в силу теоремы 3.3.2 эти векторы будут линейно зависимы.
коллинеарны. Будем считать, что среди них нет нулевого вектора, ибо в противном случае в силу теоремы 3.3.2 эти векторы будут линейно зависимы.
Если ненулевые векторы  и
и  коллинеарны, то в соответствии с теоремой 3.1.2 вектор
коллинеарны, то в соответствии с теоремой 3.1.2 вектор  представим в виде
представим в виде  =
= . Тогда
. Тогда  + (– 1)
+ (– 1)  =
= 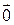 , что и означает линейную зависимость векторов
, что и означает линейную зависимость векторов  и
и  .
.
Следствие 3. 4.1. Любые два неколлинеарных вектора  и
и  являются линейно независимыми.
являются линейно независимыми.
Теорема 3.4.2. Три вектора в линейном пространстве V 3 являются линейно зависимыми тогда и только тогда, когда они компланарны.
Доказательство. Необходимость. Пусть векторы  ,
,  ,
, 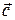 линейно зависимы, следовательно, существуют такие вещественные числа a, b, d, что
линейно зависимы, следовательно, существуют такие вещественные числа a, b, d, что 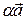 +
+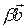 +
+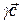 =
=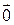 , при этом хотя бы одно из них не равно нулю. Допустим для определенности, что g ¹ 0. Тогда
, при этом хотя бы одно из них не равно нулю. Допустим для определенности, что g ¹ 0. Тогда
 +
+ +
+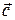 =
=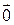
или
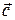 =
=
 .
.
Векторы  ,
,  коллинеарны соответственно векторам
коллинеарны соответственно векторам  и
и  , а их сумма, т. е. вектор
, а их сумма, т. е. вектор 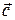 , будет лежать в плоскости векторов
, будет лежать в плоскости векторов  и
и  . Следовательно, векторы
. Следовательно, векторы  ,
,  ,
, 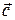 компланарны.
компланарны.
Достаточность. Пусть векторы  ,
,  ,
, 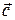 компланарны. Будем считать, что среди них нет ни одной пары коллинеарных, ибо в противном случае в силу теоремы 3.3.3 три данных вектора будут линейно зависимыми.
компланарны. Будем считать, что среди них нет ни одной пары коллинеарных, ибо в противном случае в силу теоремы 3.3.3 три данных вектора будут линейно зависимыми.
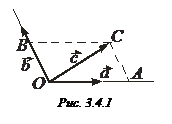 Приведем векторы
Приведем векторы  ,
,  ,
, 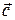 к общему началу О (рис. 3.4.1). Проведем через точку С прямую С
к общему началу О (рис. 3.4.1). Проведем через точку С прямую С  , параллельную вектору
, параллельную вектору  и пересекающую прямую О
и пересекающую прямую О  в точке В. Далее параллельно вектору
в точке В. Далее параллельно вектору  спроектируем точку С на прямую О
спроектируем точку С на прямую О  . Векторы
. Векторы 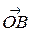 и
и  , а также
, а также 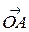 и
и  коллинеарны. Тогда в силу теоремы 3.1.2
коллинеарны. Тогда в силу теоремы 3.1.2  ,
,  =
=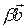 . Однако
. Однако 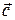 =
= +
+ =
=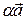 +
+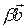 , откуда
, откуда 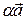 +
+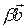 + (–1)
+ (–1)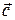 =
= 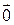 , что и означает линейную зависимость векторов
, что и означает линейную зависимость векторов  ,
,  ,
, 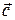 .
.
Следствие 3. 4.2. Если векторы  ,
,  ,
, 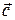 некомпланарны, то они линейно независимы в V 3.
некомпланарны, то они линейно независимы в V 3.
Следствие 3. 4.3. Каковы бы ни были два неколлинеарных вектора  ,
,  на плоскости, всякий третий вектор
на плоскости, всякий третий вектор 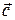 , лежащий в этой же плоскости, может быть разложен по векторам
, лежащий в этой же плоскости, может быть разложен по векторам  и
и  в виде
в виде 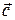 =
=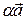 +
+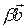 .
.
Теорема 3.4.3. Любые четыре вектора линейного пространства V 3 линейно зависимы.
Доказательство. Пусть  ,
,  ,
, 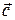 ,
, 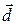 — произвольные векторы в пространстве V 3. Будем считать, что среди этих векторов никакие три не являются компланарными, ибо в противном случае данные четыре вектора будут заведомо линейно зависимы.
— произвольные векторы в пространстве V 3. Будем считать, что среди этих векторов никакие три не являются компланарными, ибо в противном случае данные четыре вектора будут заведомо линейно зависимы.
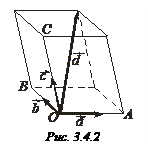 Приведем все векторы к общему началу О (рис. 3.4.2). Проведем через конец вектора
Приведем все векторы к общему началу О (рис. 3.4.2). Проведем через конец вектора 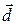 плоскости параллельные плоскостям, в которых лежат пары векторов
плоскости параллельные плоскостям, в которых лежат пары векторов 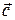 и
и  ,
,  и
и 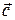 ,
,  и
и  соответственно. Обозначим через A, B, C соответственно точки пересечения указанных плоскостей с прямыми О
соответственно. Обозначим через A, B, C соответственно точки пересечения указанных плоскостей с прямыми О  ,
,
О  , О
, О 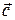 .
.
Векторы 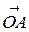 и
и  ,
,  и
и  ,
,  и
и 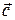 коллинеарны. Поэтому по теореме 3.1.2
коллинеарны. Поэтому по теореме 3.1.2 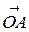 =
=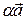 ,
,  =
=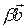 ,
,  =
=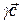 . Однако
. Однако 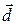 =
=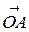 +
+ +
+ , откуда
, откуда 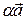 +
+ 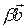 +
+ 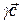 + (– 1)
+ (– 1) 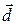 =
=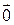 , что и означает линейную зависимость векторов
, что и означает линейную зависимость векторов  ,
,  ,
, 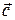 ,
, 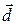 .
.
Следствие 3.4.4. Каковы бы ни были три некомпланарных вектора линейного пространства V 3, любой четвертый вектор из этого пространства может быть разложен по этим векторам.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 6962; Нарушение авторских прав?; Мы поможем в написании вашей работы!