
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрический смысл систем линейных уравнений
|
|
|
|
Пусть прямая  проходит через точку
проходит через точку 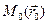 и имеет направляющий вектор
и имеет направляющий вектор  (рис.4.6.1).
(рис.4.6.1).

Рис. 4.6.1.
Тогда радиус-вектор 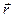 произвольной точки
произвольной точки 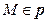 можно вычислить по формуле
можно вычислить по формуле
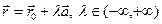 . (4.6.1)
. (4.6.1)
В заданной декартовой прямоугольной системе координат  имеем
имеем 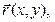
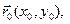
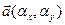 , поэтому из (4.6.1) получаем
, поэтому из (4.6.1) получаем
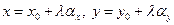 ,
, 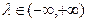 . (4.6.2)
. (4.6.2)
Соотношения (4.6.2) называются параметрическими уравнениями прямой на плоскости. Выражая из равенств (4.6.2) параметр 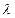 , и, приравнивая правые части, получаем
, и, приравнивая правые части, получаем
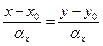 . (4.6.3)
. (4.6.3)
Соотношение (4.6.3) называется каноническим уравнением прямой на плоскости.
С другой стороны, очевидно, имеем 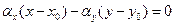 , т. е.
, т. е.
 , (4.6.4)
, (4.6.4)
где 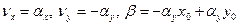 . Следовательно, одно линейное уравнение с двумя неизвестными определяет прямую на плоскости.
. Следовательно, одно линейное уравнение с двумя неизвестными определяет прямую на плоскости.
Определение 4.6.1. Вектор  называется нормальным вектором прямой.
называется нормальным вектором прямой.
Так как скалярное произведение 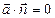 , то нормальный вектор перпендикулярен любому вектору, лежащему на прямой
, то нормальный вектор перпендикулярен любому вектору, лежащему на прямой  .
.
Рассмотрим теперь систему линейных уравнений
 (4.6.5)
(4.6.5)
Каждое уравнение системы определяет прямую на плоскости. Нормальные векторы этих прямых 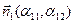 и
и 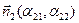 . Если
. Если  , то векторы
, то векторы 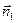 и
и  не являются коллинеарными, при этом (4.6.5) имеет единственное решение, определяющее точку на плоскости.
не являются коллинеарными, при этом (4.6.5) имеет единственное решение, определяющее точку на плоскости.
В том случае, когда 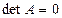 , получаем
, получаем
 , (4.6.6)
, (4.6.6)
следовательно, векторы 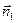 и
и  коллинеарны. Если, кроме того,
коллинеарны. Если, кроме того,
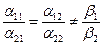 ,
,
то ранг матрицы системы равен 1, а ранг расширенной матрицы равен 2. Поэтому система (4.6.5) не имеет решения, что означает параллельность прямых.
Когда справедливо соотношение
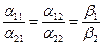 ,
,
то ранг матрицы системы равен рангу расширенной матрицы и система (4.6.5) имеет бесконечное число решений, что отвечает случаю совпадения двух прямых.
Пусть точки 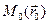 и
и 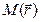 лежат в некоторой плоскости
лежат в некоторой плоскости 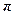 . Допустим, что
. Допустим, что  и
и 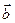 два неколлинеарных вектора, лежащих в указанной плоскости (рис. 4.6.2).
два неколлинеарных вектора, лежащих в указанной плоскости (рис. 4.6.2).

Рис.4.6.2
Как известно, любой третий вектор в этой плоскости можно разложить по векторам  и
и 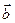 как по базису. Поэтому
как по базису. Поэтому 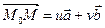 , следовательно, имеем уравнение
, следовательно, имеем уравнение
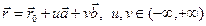 . (4.6.7)
. (4.6.7)
Уравнение (4.6.7) называется векторно-параметрическим уравнением плоскости. Оно определяет правило вычисления радиус-вектора произвольной точки плоскости 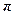 .
.
В фиксированной декартовой прямоугольной системе координат Oxyz 
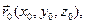
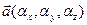 ,
,  . Поэтому в соответствии с (4.6.7) получаем
. Поэтому в соответствии с (4.6.7) получаем
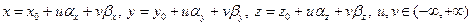 . (4.6.8)
. (4.6.8)
Соотношения (4.6.8) называются параметрическими уравнениями плоскости, причем u и v — параметры, определяющие положение точки в плоскости 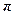 .
.
По условию векторы  и
и 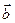 неколлинеарны, а тогда их координаты непропорциональны. Допустим, например, что
неколлинеарны, а тогда их координаты непропорциональны. Допустим, например, что 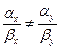 , т. е.
, т. е. 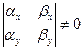 . Из первых двух соотношений (4.6.8) с помощью формулы Крамера однозначно определяются выражения для параметров u и v:
. Из первых двух соотношений (4.6.8) с помощью формулы Крамера однозначно определяются выражения для параметров u и v:
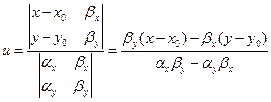 ,
, 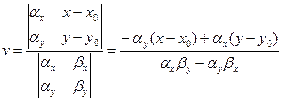 .
.
Подставляя полученные выражения в третье соотношение формул (4.6.8), получаем
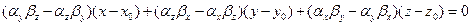 .
.
Если ввести обозначения  , то уравнение плоскости, проходящей через точку
, то уравнение плоскости, проходящей через точку 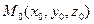 , принимает вид
, принимает вид
 ,
,
отсюда имеем
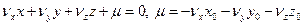 . (4.6.9)
. (4.6.9)
Соотношение (4.6.9) называется общим уравнением плоскости. Вектор  называется нормальным вектором плоскости и обладает тем свойством, что перпендикулярен любому вектору, лежащему в данной плоскости, что непосредственно следует из формулы (4.6.9). Таким образом, линейное уравнение с тремя неизвестными определяет плоскость.
называется нормальным вектором плоскости и обладает тем свойством, что перпендикулярен любому вектору, лежащему в данной плоскости, что непосредственно следует из формулы (4.6.9). Таким образом, линейное уравнение с тремя неизвестными определяет плоскость.
В векторной записи общее уравнение имеет вид  , откуда получаем
, откуда получаем
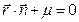 , где
, где  . (4.6.10)
. (4.6.10)
Уравнение (4.6.10) называется общим векторным уравнением плоскости.
Заметим, что 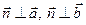 , следовательно, по определению векторного произведения можно принять
, следовательно, по определению векторного произведения можно принять 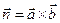 , а поэтому получаем следующее уравнение плоскости, проходящей через точку
, а поэтому получаем следующее уравнение плоскости, проходящей через точку 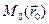 :
:
 .
.
Векторно-параметрическое уравнение (4.6.1) прямой в фиксированной ДПСК в пространстве определяет параметрические уравнения указанной прямой:
 , (4.6.11)
, (4.6.11)
где 

 .
.
Направляющий вектор 
 , следовательно, среди его координат обязательно есть отличные от нуля. Пусть для определенности
, следовательно, среди его координат обязательно есть отличные от нуля. Пусть для определенности  . Выражая параметр l из первого соотношения, и, подставляя в два других, получаем систему линейных уравнений
. Выражая параметр l из первого соотношения, и, подставляя в два других, получаем систему линейных уравнений
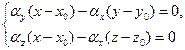
или
 (4.6.12)
(4.6.12)
где 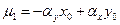 ,
, 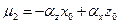 . Таким образом, система двух линейных уравнений с тремя неизвестными (4.6.12) является общим уравнением прямой в пространстве.
. Таким образом, система двух линейных уравнений с тремя неизвестными (4.6.12) является общим уравнением прямой в пространстве.
Выражая параметр l из каждого соотношения (4.6.11), получаем каноническое уравнение прямой в пространстве, проходящей через точку 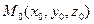 , с направляющим вектором
, с направляющим вектором 
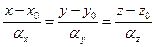 . (4.6.13)
. (4.6.13)
Заметим, что если какая-либо координата направляющего вектора равна нулю, то в соответствии с правилами пропорций необходимо приравнять нулю соответствующий числитель в (4.6.13).
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 2921; Нарушение авторских прав?; Мы поможем в написании вашей работы!