Учетный или дисконтный множитель

Пример 1.11. Через 5 лет предприятию будет выплачена сумма 1000 000 руб. Определить ее современную стоимость, при условии, что применяется ставка сложных процентов 10 % годовых.

Решение. По формуле (1.2.7) находим

Р = 1 000 000*(1+0,10) ^(-5)= 620 921,32 руб.

Если проценты начисляются m раз в году, то получим

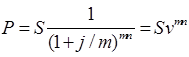, (1.2.9)

где

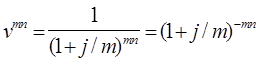(1.2.10)

дисконтный множитель.

Величину P, полученную дисконтированием S, называют современной или текущей стоимостью или приведенной величиной S. Суммы P и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме P, выплачиваемой в настоящий момент.

Разность D=S-P называют дисконтом.

Банковский учет. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле

P=S(1-d_сл)ⁿ, (1.2.11)

где d_сл - сложная годовая учетная ставка.

Дисконт в этом случае равен

D=S-P=S-S(1-d_сл)ⁿ=S[1-(1-d_сл)ⁿ]. (1.2.12)

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.

Пример 1.12. Через 5 лет по векселю должна быть выплачена сумма 1 000 000 руб. Банк учел вексель по сложной учетной ставке 10 % годовых. Определить дисконт.

Решение. По формуле (1.2.11) находим

Р = 1 000 000*(1 - 0,10) ⁵= 590 490,00 руб.

D = S – P = 1 000 000 – 590 490 = 409 510 руб.

Дата добавления: 2014-01-05