Потоки платежей

Очень часто в контрактах финансового характера предусматриваются не отдельные разовые платежи, а серию платежей, распределенных во времени. Примерами могут быть регулярные выплаты с целью погашения долгосрочного кредита вместе с начисленными на него процентами, периодические взносы на расчетный счет, на котором формируется некоторый фонд различного назначения (инвестиционный, пенсионный, страховой, резервный, накопительный и т.д.), дивиденды, выплачиваемые по ценным бумагам, выплаты пенсий из пенсионного фонда и пр. Ряд последовательных выплат и поступлений называют потоком платежей. Выплаты представляются отрицательными величинами, а поступления - положительными.

Обобщающими характеристиками потока платежей являются наращенная сумма и современная величина. Каждая из этих характеристик является числом.

Наращенная сумма потока платежей это сумма всех членов последовательности платежей с начисленными на них процентами к концу срока ренты.

Под современной величиной потока платежей понимают сумму всех его членов, дисконтированных (приведенных) на некоторый момент времени, совпадающий с началом потока платежей или предшествующий ему.

Конкретный смысл этих обобщающих характеристик определяется природой потока платежей, причиной, его порождающей. Например, наращенная сумма может представлять собой итоговый размер формируемого инвестиционного или какого-либо другого фонда, общую сумму задолженности. Современная величина может характеризовать приведенную прибыль, приведенные издержки.

1.3.1. Финансовые ренты и их классификация. Поток платежей, все члены которого положительные величины, а временные интервалы постоянны, называют финансовой рентой или аннуитетом.

Финансовая рента имеет следующие параметры: член ренты - величина каждого отдельного платежа, период ренты - временной интервал между двумя соседними платежами, срок ренты - время, измеренное от начала финансовой ренты до конца ее последнего периода, процентная ставка - ставка, используемая при наращении или дисконтировании платежей, образующих ренту.

Виды финансовых рент. Классификация рент может быть произведена по различным признакам.

В зависимости от продолжительности периода, ренты делят на годовые и p-срочные, где p - число выплат в году.

По числу начислений процентов различают ренты с начислением один раз в году, m раз или непрерывно. Моменты начисления процентов могут не совпадать с моментами рентных платежей.

По величине членов различают постоянные (с равными членами)и переменные ренты. Если размеры платежей изменяются по какому-либо математическому закону, то часто появляется возможность вывести стандартные формулы, значительно упрощающие расчеты.

По вероятности выплаты членов различают ренты верные и условные. Верные ренты подлежат безусловной выплате, например, при погашении кредита. Выплата условной ренты ставится в зависимость от наступления некоторого случайного события. Поэтому число ее членов заранее неизвестно. Например, число выплат пенсий зависит от продолжительности жизни пенсионера.

По числу членов различают ренты с конечным числом членов или ограниченные и бесконечные или вечные. В качестве вечной ренты можно рассматривать выплаты по облигационным займам с неограниченными или не фиксированными сроками.

В зависимости от наличия сдвига момента начала ренты по отношению к началу действия контракта или какому-либо другому моменту ренты подразделяются на немедленные и отложенные или отсроченные. Срок немедленных рент начинается сразу, а у отложенных запаздывает.

Ренты различают по моменту выплаты платежей. Если платежи осуществляются в конце каждого периода, то такие ренты называются обычными или постнумерандо. Если же выплаты производятся в начале каждого периода, то ренты называются пренумерандо. Иногда предусматриваются платежи в середине каждого периода.

Анализ потоков платежей в большинстве случаев предполагает расчет наращенной суммы или современной величины ренты.

1.3.2. Формулы наращенной суммы. Обычная годовая рента. Пусть в конце каждого года в течение n лет на расчетный счет вносится по R рублей, сложные проценты начисляются один раз в год по ставке i. В этом случае первый взнос к концу срока ренты возрастет до величины R(1+i)^n-1, так как на сумму R проценты начислялись в течение n-1 года. Второй взнос увеличится до R(1+i)^n-2 и т.д. На последний взнос проценты не начисляются. Таким образом, в конце срока ренты ее наращенная сумма будет равна сумме членов геометрической прогрессии

S =R+R(1+i)+R(1+i)²+... + R(1+i)^n-1,

в которой первый член равен R, знаменатель (1+i), число членов n. Эта сумма равна

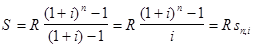, (1.3.1)

где

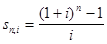(1.3.2)

называется коэффициентом наращения ренты. Он зависит только от срока ренты n и уровня процентной ставки i.

Пример 1.13. В течение 3 лет на расчетный счет в конце каждого года поступает по 10 млн. руб., на которые 1 раз в год начисляются проценты по сложной годовой ставке 10%. Требуется определить сумму на расчетном счете к концу указанного срока.

Решение. По формуле (1.3.1) находим

S = 10*[(1+0,1) ³ – 1] / 0,1 = 33.100 млн. руб.

Годовая рента, начисление процентов m раз в году. Посмотрим как усложнится формула, если предположить теперь, что платежи делают один раз в конце года, а проценты начисляют m раз в году. Это означает, что применяется каждый раз ставка j/m, где j - номинальная ставка процентов. Тогда члены ренты с начисленными до конца срока процентами имеют вид

R(1+j/m)^m(n-1), R(1+j/m)^m(n-2),..., R.

Если прочитать предыдущую строку справа налево, то нетрудно увидеть, что перед нами опять геометрическая прогрессия, первым членом которой является R, знаменателем (1+j/m)^m, а число членов n. Сумма членов этой прогрессии и будет наращенной суммой ренты. Она равна

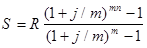. (1.3.3)

Пример 1.14. В течение 3 лет на расчетный счет в конце каждого года поступает по 10 млн. руб., на которые ежеквартально (m=4) начисляются проценты по сложной годовой ставке 10%. Требуется определить сумму на расчетном счете к концу указанного срока.

Решение. По формуле (1.3.3) находим

S = 10*[(1+0,1/4)^(3*4) – 1] / [(1+0,1/4) ⁴ – 1] = 33.222 млн. руб.

Рента p -срочная, m =1. Найдем наращенную сумму при условии, что рента выплачивается p раз в году равными платежами, а проценты начисляются один раз в конце года. Если R - годовая сумма платежей, то размер отдельного платежа равен R/p. Тогда последовательность платежей с начисленными до конца срока процентами также представляет собой геометрическую прогрессию, записанную в обратном порядке,

,

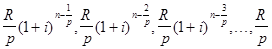у которой первый член R/p, знаменатель (1+i)^1/p, общее число членов np. Тогда наращенная сумма рассматриваемой ренты равна сумме членов этой геометрической прогрессии

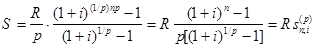, (1.3.4)

где

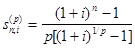(1.3.5)

коэффициент наращения p -срочной ренты при m=1.

Пример 1.15. В течение 3 лет на расчетный счет в конце каждого квартала поступают платежи равными долями из расчета 10 млн. руб. в год (т.е. по 10/4 млн. руб. в квартал), на которые в конце года начисляются проценты по сложной ставке 10% годовых. Требуется определить сумму на расчетном счете к концу указанного срока.

Решение. По формуле (1.3.4) находим

S = (10/4)*[(1+0,1) ³ – 1] / [(1+0,1) ^(1/4)– 1] = 34.317 млн. руб.

Рента p -срочная, p=m. В контрактах часто начисление процентов и поступление платежа совпадают во времени. Таким образом число платежей p в году и число начислений процентов m совпадают, т.е. p=m. Тогда для получения формулы расчета наращенной суммы можно воспользоваться аналогией с годовой рентой и одноразовым начислением процентов в конце года, для которой

.

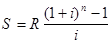Различие будет лишь в том, что все параметры теперь характеризуют ставку и платеж за период, а не за год.

Таким образом получаем

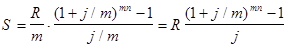. (1.3.6)

Пример 1.16. В течение 3 лет на расчетный счет в конце каждого квартала поступают платежи равными долями из расчета 10 млн. руб. в год (т.е. по 10/4 млн. руб. в квартал), на которые ежеквартально начисляются проценты по сложной ставке 10% годовых. Требуется определить сумму на расчетном счете к концу указанного срока.

Решение. По формуле (1.3.6) находим

S = 10*[(1+0,1/4) ^(3*4) – 1] / 0,1 = 34.489 млн. руб.

Рента p -срочная, p³1, m³1. Это самый общий случай p -срочной ренты с начислением процентов m раз в году, причем, возможно p¹m.

Первый член ренты R/p, уплаченный спустя 1/p года после начала, составит к концу срока вместе с начисленными на него процентами

.

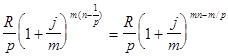Второй член ренты к концу срока возрастет до

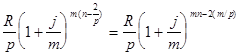
и т.д. Последний член этой записанной в обратном порядке геометрической прогрессии равен R/p, ее знаменатель (1+j/m)^m/p, число членов nm.

В результате получаем наращенную сумму

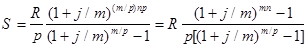. (1.3.7)

Отметим, что из нее легко получить все рассмотренные выше частные случаи, задавая соответствующие значения p и m.

Пример 1.17. В течение 3 лет на расчетный счет в конце каждого квартала поступают платежи (p=4) равными долями из расчета 10 млн. руб. в год (т.е. по 10/4 млн. руб. в квартал), на которые ежемесячно (m=12) начисляются проценты по сложной ставке 10% годовых. Требуется определить сумму на расчетном счете к концу указанного срока.

Решение. По формуле (1.3.7) находим

S = (10/4)*[(1+0,10/4) ^(3*4)–1]/[(1+0,10/4)^(12/4)–1]=34.5296 млн. руб.

1.3.3. Формулы современной величины. Обычная годовая рента. Пусть член годовой ренты равен R, процентная ставка i, проценты начисляются один раз в конце года, срок ренты n. Тогда дисконтированная величина первого платежа равна

,

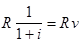где

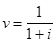- дисконтный множитель.

Приведенная к началу ренты величина второго платежа равна Rv² и т.д. В итоге приведенные величины образуют геометрическую прогрессию: Rv, Rv², Rv³,..., Rvⁿ, сумма которой равна

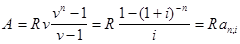, (1.3.8)

где

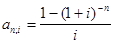(1.3.9)

- коэффициент приведения ренты.

Как видим, коэффициент приведения ренты зависит только от двух параметров: срока ренты n и процентной ставки i.

Пример 1.18. В течение 3 лет на расчетный счет в конце каждого года поступает по 10 млн. руб. Ежегодное дисконтирование производится по сложной процентной ставке 10% годовых. Определить современную стоимость ренты..

Решение. По формуле (1.3.8) находим

А = 10 * [1- (1+0.1)^(-3)]/0.1 =24.868 млн. руб

Рента p -срочная, p³1, m³1. Аналогичные рассуждения позволяют получить формулу для расчета современной величины ренты в самом общем случае для произвольных значений p и m

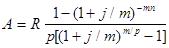, (1.3.10)

от которой нетрудно перейти к частным случаям при различных p и m.

Дата добавления: 2014-01-05