Определение скорости и ускорения произвольной точки тела

Из рисунка ясно, что

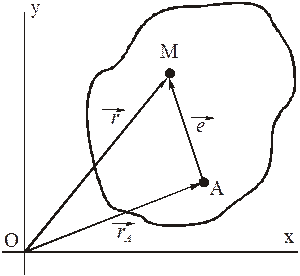
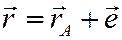
Если уравнения движения (1) фигуры заданы, то

поэтому радиус-вектор точки М – известная функция от времени t.

2.1 Определение скорости точки плоской фигуры.

Тогда

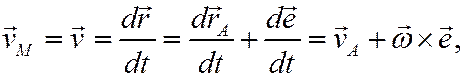
где

угловая скорость плоской фигуры.

Вектор – это скорость полюса А, которая может быть найдена по закону движения (1)

Выражение 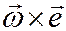определяет скорость точки М при её вращении вокруг полюса А, который считается как бы неподвижным (вращательная часть движения плоской фигуры!). Эту скорость обозначают

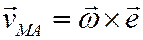
и называют скоростью точки М при её вращении вокруг полюса А.

Окончательно для вектора скорости точки М плоской фигуры получаем выражение

Т.к. в случае плоского движения всегда 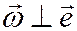, то модуль скорости точки М при вращении вокруг полюса равен

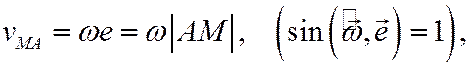
а вектор 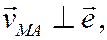лежит в плоскости фигуры и направлен в сторону её вращения.

Т.к. согласно (4) вектор скорости точки М фигуры равен векторной сумме двух векторов, то он определяется геометрически

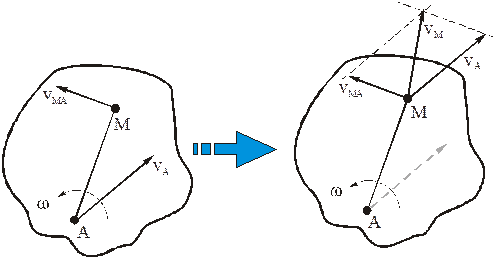
по правилу параллелограмма. Модуль может быть найден либо по теореме косинусов

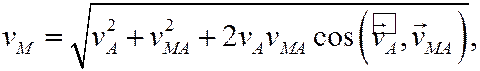
либо через проекции формулы (4) на какие-то оси x и y:

2.2 Определение ускорения точки плоской фигуры.

Аналогично определению скорости точки фигуры, имеем

В этой цепочке равенств:

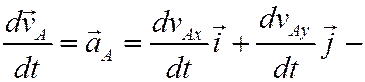
вектор ускорения полюса, который может быть найден по закону движения плоской фигуры (1);

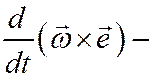
вектор ускорения точки М фигуры при её вращении вокруг «как бы неподвижного полюса», который, как и при вращательном движении тела, находится в виде двух составляющих:

касательного

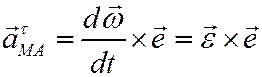
и нормального

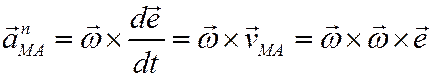
ускорений. Поэтому окончательно получаем, что вектор ускорения точки плоской фигуры равен

В равенстве (8) вектор касательного ускорения точки при её вращении вокруг полюса А определён формулой

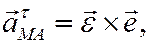
его модуль находится как

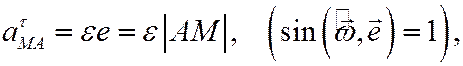
а направление 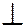отрезку АМ, вектор лежит в плоскости фигуры и направлен в сторону углового ускорения e фигуры.

Вектор нормального ускорения точки при её вращении вокруг полюса А равен

его модуль

а направлен вектор всегда вдоль отрезка АМ от точки М к полюсу А.

Т.к., согласно (8), вектор ускорения равен сумме трёх векторов, то геометрически он определяется по правилу векторного многоугольника

,

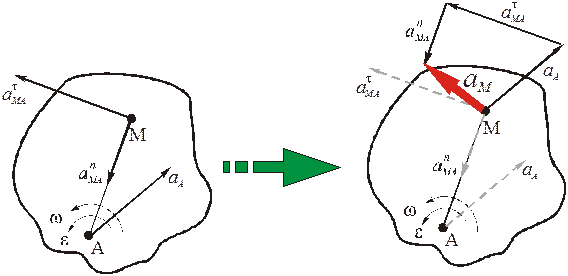а аналитически – по проекциям на какие-либо выбранные оси координат:

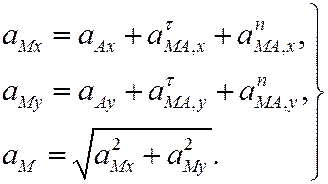
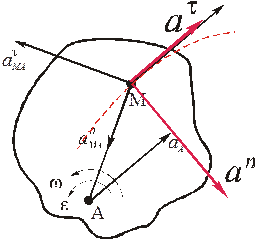
Замечание. Составляющие ускорения точки плоской фигуры в формуле (8) нельзя называть касательным и нормальным ускорениями точки. Это – именно «касательное ускорение при вращении вокруг полюса» и «нормальное ускорение при вращении вокруг полюса». Они не совпадают с «настоящими» касательным и нормальным ускорениями!

Дата добавления: 2014-01-05