Лекция 5

Сложение скоростей и ускорений точки при сложном движении

Вопросы лекции

1. Сложение скоростей точки.

2. Сложение ускорений точки (кинематическая теорема Кориолиса).

3. Ускорение Кориолиса.

Тарг, 2009: с. 156 – 168.

1. Сложение скоростей точки.

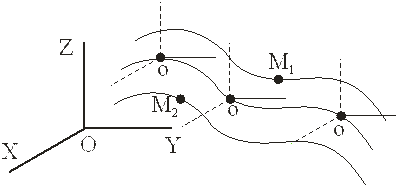
Согласно рисунку прошлой лекции

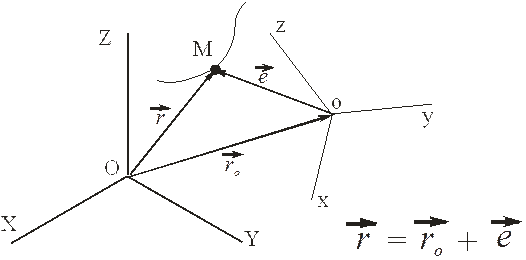
имеем

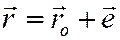
(абсолютный радиус-вектор точки равен сумме абсолютного радиус-вектора начала подвижной системы координат и относительного радиус-вектора).

По определению абсолютной скорости

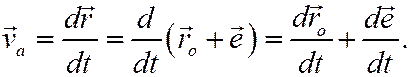
Ясно, что

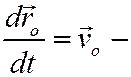
вектор абсолютной скорости точки о начала подвижной системы координат oxyz.

Второе слагаемое представляет абсолютную производную от относительного радиус-вектора. Применяем формулу Бура

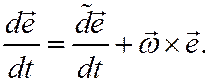
По определению

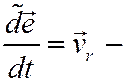
относительная скорость точки.

Следовательно, получаем

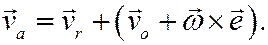
Выражение в скобках по определению есть переносная скорость точки (скорость полюса о плюс скорость точки тела при вращении вокруг полюса; модуль )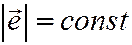

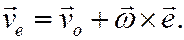
Окончательно можем записать

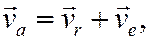
т.е. абсолютная скорость точки равна векторной сумме относительной и переносной скоростей.

При произвольном переносном движении переносная скорость определяется по формуле (3). Равенство (4) можно записывать в форме (2), расписывая переносную скорость сразу в явном виде.

Частные случаи переносного движения.

1) Переносное движение поступательное (подвижная система oxyz движется относительно неподвижной OXYZ поступательно). В этом случае 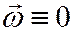, и для переносной скорости из (3) получаем

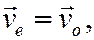
т.е. при поступательном переносном движении переносная скорость точки М в любом её положении равна скорости начала «о» подвижной системы координат.

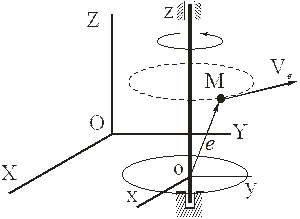
2) Переносное движение вращательное. В этом случае всегда можно начало отсчета «о» подвижной системы выбрать на оси вращения, а одну из координатных осей (например, ось z) направить вдоль оси вращения. Тогда из (3) следует

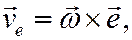
т.е. переносная скорость определяется как при вращательном движении тела по формуле Эйлера.

В остальных случаях переносного движения переносную скорость следует определять по общей формуле (3).

Так как согласно (4) при определении абсолютной скорости складывается два вектора, то определять модуль абсолютной скорости можно двумя способами.

Первый – по теореме косинусов имеем

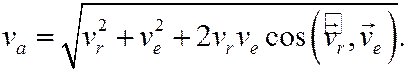
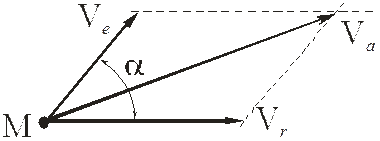
Выражение (7) является универсальным. При a = 0 (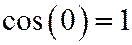) получаем

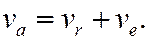
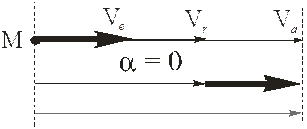
При a = 180° (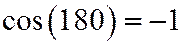) будет

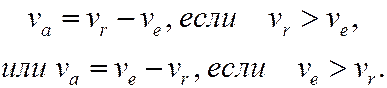
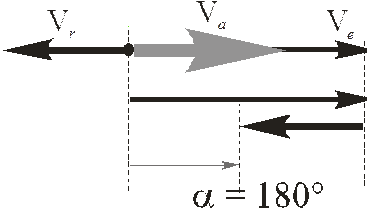
Направлен вектор 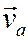в сторону большей по модулю скорости.

При a = 90° (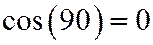) получим теорему Пифагора

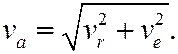
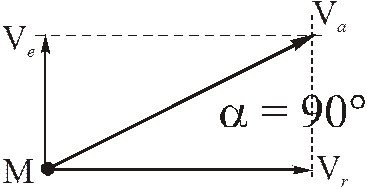
При использовании этого способа направление вектора 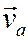абсолютной скорости находится геометрически (на картинке).

Второй способ. Выбирается какая-либо система координат (можно OXYZ, можно oxyz, можно – любую другую систему). Равенство (4) проектируется на выбранные оси:

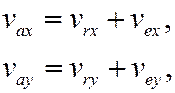
тогда модуль абсолютной скорости

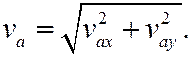
Замечание. Так как векторы 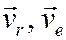– скорости точки М (векторы «исходят» из одной точки), то они всегда лежат в одной плоскости, поэтому, выбирая систему координат соответствующим образом, равенство (4) всегда достаточно спроектировать лишь на две оси координат, а не на три.

Рассмотрим пример определения абсолютных скоростей точек.

Дата добавления: 2014-01-05