Суждения об устойчивости линейной САУ

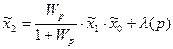(3.1)

(3.2)

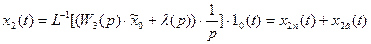(3.3)

- переходное состояние

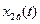- вынужденное состояние

- общее решение ОДУ без правой части.

Характер изменений во времени полностью определён характеристиками системы (или параметрами).

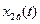- частное решение ОДУ, зависит от входного сигнала 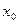и имеет характер изменений во времени такой же, как .

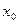Для линейной системы:

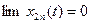(3.4)

(3.5)

(3.6)

Обычно 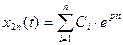(3.7)

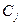- постоянная интегрирования, зависит от параметров систем и НУ.

Необходимое и достаточное условие устойчивости:

Чтобы САУ была устойчивой, необходимо и достаточно, чтобы все вещественные части корней характеристического уравнения 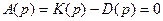были бы меньше нуля.

Соотношение между погрешностями системы, при которых хотя бы один корень попадает на мнимую ось, определяет границу устойчивости.

Вывод: чтобы узнать, устойчива система или нет, необязательно знать вещественную часть, а необходимо знать знак вещественной части.

Правила, которые позволяют определить устойчивость системы, носят название критериев устойчивости.

- критерий Михайлова

- критерий Гурвица

- критерий Гаусса

- критерий Найквиста

- метод Д-разбиения

- метод корневого годографа

Дата добавления: 2014-01-05