Линией действия

Точкой приложения;

Направлением;

Модулем;

Сила может быть представлена геометрически (на рисунке)

.

Силу (как и любой другой вектор) можно представлять аналитически. Для этого нужно выбрать три взаимно перпендикулярных единичных вектора

(предполагается, что их направления заданы, например, на юг, на восток и вверх, или каким-то иным способом). С этими единичными векторами обычно связывают координатные оси x, y, z соответственно, а введённые векторы задают положительные направления этих осей.

Тогда вектор силы определяется тройкой чисел

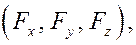
которые равны проекциям вектора силы не соответствующие оси (на направления единичных векторов ):

.

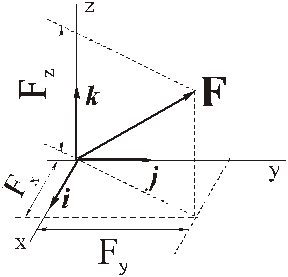Если в выражении (1) все три числа заданы, то модуль силы определится по формуле

а направление найдётся с помощью направляющих косинусов: косинусов углов, которые образует вектор с положительными направлениями осей:

где F – модуль силы (2).

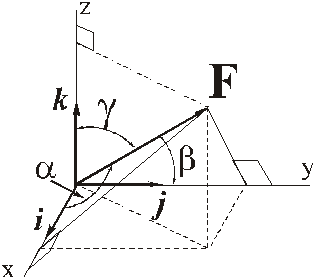
Замечания. 1) При аналитическом задании вектора силы точка её приложения указывается отдельно, например, с помощью координат , а вектор силы определяется равенствами (1) – (3), т.к. систему координат всегда можно параллельно перенести в любую точку.

2) Вектор силы вместо (1) можно записывать в виде

что часто используется на практике. Коэффициенты при единичных векторах в (4) – то же самое, что и в (1): проекции вектора на соответствующие оси.

3) Часто при задании вектора силы указывается угол 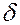между вектором силы и плоскостью Oxy, и угол 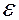между проекцией силы на плоскость Oxy и осью Ox.

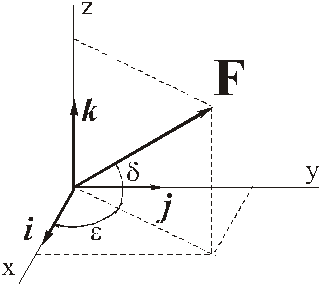
Тогда для определения проекций (1) сначала проектируем силу на плоскость Oxy

а затем на оси x и y:

Проекция силы на ось z находится сразу:

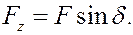
Сравнивая полученные выражения с равенствами (3) можем заключить, что

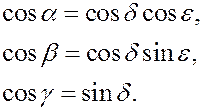
Моментом силы относительно центра О называется вектор, равный векторному произведению радиус-вектора точки приложения силы на вектор силы.

Моментом силы относительно ос и называется проекция на эту ось вектора момента силы относительно какой-либо точки оси.

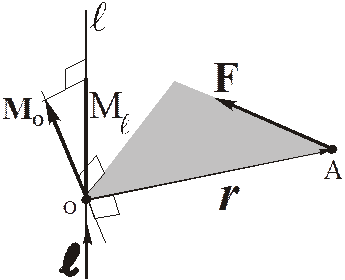
Если через 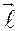обозначить единичный вектор оси, то

Две равные по модулю, противоположно направленные силы и параллельные силы называются парой сил.

Вектор, равный

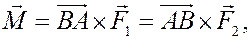
называется моментом пары сил.

Согласно (9)

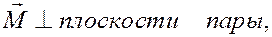
направлен так, что с его конца вращение пары происходит против часовой стрелки. Модуль момента пары

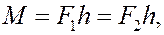
где h – плечо пары сил.

Аксиомы (законы) динамики.

1) Закон инерции.

Если на материальную точку не действуют никакие силы, то она движется равномерно и прямолинейно, или находится в покое.

Системы отсчёта, в которых этот закон справедлив, называют инерциальными.

Системы отсчёта, в которых закон инерции не выполняется, носят название неинерциальных.

2) Основной закон динамики (второй закон Ньютона).

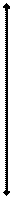В любой инерциальной системе отсчёта сила, действующая на материальную точку, сообщает ей ускорение, модуль которого пропорционален модулю силы, а направление совпадает с направлением силы.

Коэффициент пропорциональности в (5) называется мерой инерции точки. Меру инерции отождествляют с количеством вещества, содержащегося в точке, т.е. с массой точки.

3) Принцип равенства действия и противодействия (третий закон Ньютона).

Если объект А действует на объект В с силой , то объект В действует на объект А с силой 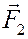, равной по величине, противоположно направленной и имеющей ту же линию действия.

4) Принцип независимости действия сил.

Ускорение, которое приобретёт точка под действием нескольких сил одновременно, равно векторной сумме ускорений, которые приобрела бы точка под действием каждой силы по отдельности.

Из четвёртого закона вытекает важное следствие, которое удобно применять на практике: в основном законе динамики силу 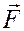можно считать суммой всех сил, действующих на точку

ЛИТЕРАТУРА

Дата добавления: 2014-01-05