Дополнительная

ОСНОВНАЯ

1. Тарг С.М. Краткий курс теоретической механики. – М.: Высшая школа, 2002, 416с.

2. Никитин Н.Н. Курс теоретической механики. – М.: Высшая школа, 1990, 607с.

3. Яблонский А.А., Никифорова В.М. Курс теоретической механики. – СПб.: Лань, 2002, 764с.

4. Мещерский И.В. Задачи по теоретической механике. – СПб.: Лань, 2002, 448с.

5. Яблонский А.А. Сборник заданий для курсовых работ по теоретической механике. – М. Интеграл-пресс, 2002. – 384 с.

6. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. – СПб.: Лань, 1995, 669 c.

1. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. – СПб.:Лань, 2002, 729с.

2. Старжинский В.М. Теоретическая механика. – М.: Наука, 1980, 464с.

3. Яблонский А.А., Норейко С.С. Курс теории колебаний. – М.: Высшая школа, 1975, 248с.

4. Бутенин Н.В., Фуфаев Н.А. Введение в аналитическую механику. – М.: Наука, 1991, 255с.

2. Дифференциальное уравнение движения материальной точки.

Пусть материальная точка массы m движется относительно инерциальной системы отсчёта под действием силы

Пусть движение точки задано векторным способом .

Согласно основному закону динамики (2-ому закону Ньютона)

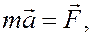
а из кинематики точки известно, что при векторном способе задания движения

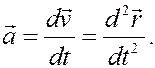
Следовательно, получаем

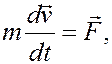
или

Равенства (1) и (2) содержат производные и носят названия дифференциальных равенств. В механике эти равенства обычно называют дифференциальными уравнениями движения материальной точки.

На практике эти векторные уравнения обычно записывают в проекциях на оси той или иной системы координат. В случае декартовой системы координат будем иметь.

При движении в пространстве:

или

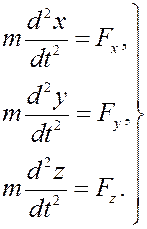
При движении точки в одной плоскости (эту плоскость совмещаем с координатной плоскостью Oxy).

или

В случае движения точки вдоль прямой (координатной оси Ox) получим

Если движение точки задано естественным способом, то равенства (1), или (2), нужно проектировать на оси естественного трёхгранника: касательную t, главную нормаль n и бинормаль b. Вспоминая проекции ускорения точки на эти оси, получим из (1), или (2)

Равенства (3) – (8) используются для решения всех задач динамики точки.

3. Первая и вторая задачи динамики.

Все возможные задачи динамики можно разделить на две группы, которые и образуют первую и вторую задачи динамики.

Первая задача динамики: по заданной массе m точки и закону её движения определить силу, действующую на точку.

Кратко.

Дано: m, .

Найти: .

Если речь идет об определении силы, как функции от времени, то решение этой задачи очень простое: согласно уравнению (2)

нужно вычислить вторую производную от известной функции 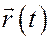, умножить её на массу m точки, – это и будет вектор силы, действующей на точку.

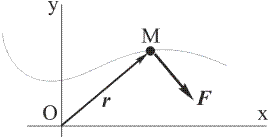
Пример. Точка массы m движется в плоскости Oxy согласно уравнениям

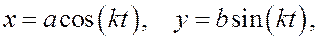
где a, b, k – некоторые постоянные числа. Определить силу, действующую на эту точку.

Решение. Имеем согласно (6):

Находим вторые производные от функций

Умножаем эти производные на массу точки и получаем

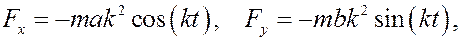
следовательно, вектор силы имеет вид

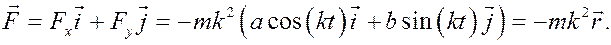
Вторая задача динамики. По заданной массе m точки и всем действующим на точку силам 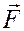найти закон движения этой точки .

Кратко.

Дано: m; .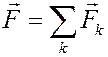

Найти: .

Согласно равенству (1), или (2), решение второй задачи связано с интегрированием дифференциального уравнения, т.к. в этих равенствах неизвестная функция входит под знак производной.

Чисто формально из (1) имеем

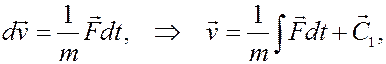
а, вспоминая, что

далее аналогично получаем

В связи с этой формальной процедурой возникает два вопроса:

как вычислять интегралы ;

как определять «произвольные» константы 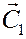и , на которые могут отличаться первообразные при вычислении неопределённых интегралов.

Способ вычисления интегралов определяется тем, от каких величин зависят силы, действующие на точку.

Силы, действующие на точку, могут быть:

§ постоянными ;

§ зависящими от времени ;

§ зависящими от положения точки ;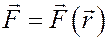

§ зависящими от скорости точки .

Для определения постоянных 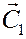и должны быть заданы начальные условия.

Начальные условия – это положение точки и её скорость, заданные в какой-то момент времени 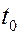, т.е.

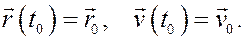
При движении точки в пространстве число начальных условий равно шести:

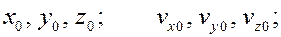
при движении на плоскости – четыре:

при движении точки вдоль одной прямой – два:

На практике чаще всего задают положение и скорость точки при t = 0, т.е. в начальный момент времени, отсюда и название – «начальные условия».

Таким образом, окончательная формулировка второй задачи динамики должна быть такой.

Вторая задача динамики. По заданной массе, всем действующим силам и начальным условиям, найти закон движения этой точки.

Во многих случаях решение 2-ой задачи динамики является очень сложным, эту задачу приходится решать чаще, чем 1-ую, поэтому иногда вторую задачу называют основной задачей динамики.

4. Решение второй (основной) задачи динамики.

Рассмотрим движение точки по прямой, вдоль которой направим координатную ось x. Пусть на точку действует сила 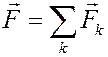, направленная вдоль этой же прямой.

Для решения задачи используем равенство (7):

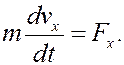
В данном случае

а начальные условия будем считать произвольными

Рассмотрим разные случаи зависимости сил от параметров .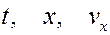

Дата добавления: 2014-01-05