Вставка в трикутник вищого класу

Вставка в трикутник вищого класу показана на рис. 2.6.

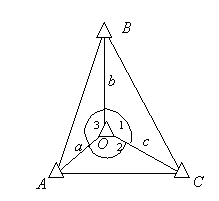
Рисунок 2.6 - Вставка в трикутник вищого класу

Відомий вчений і практик в області геодезії С.Г. Судаков, узагальнюючи свій досвід побудови основних геодезичних мереж в СРСР [8], рекомендує для визначення очікування середньої квадратичної помилки положення пункту О по відношенню до суміжних пунктів формулу:

,

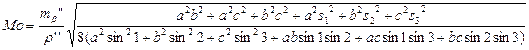(2.13)

де m_b — середня квадратична помилка вимірювання кутів;

а, в, с, s ₁, s ₂, s ₃ — довжини сторін, зняті з карти, в метрах;

1, 2, 3 — кути, зняті з карти, в градусах.

Згідно з [4], для пункту планової мережі 3 класу, величина М_O не повинна перевищувати 0,04 м.

Якщо виконується оцінка проекту вставки 4 кл., 1 або 2 розряду, то обчислюють очікувану відносну помилку 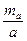визначення сторони, наприклад а (рис. 2.6)

,

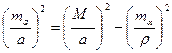(2.14)

де а — довжина сторони;

m_a — середня квадратична помилка дирекційного кута сторони а, яку знайдемо з таких міркувань:

,

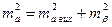де 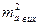— середня квадратична помилка вихідної сторони АВ;

m_b — середня квадратична помилка вимірювання кута ОАВ.

Оскільки мова іде про взаємне положення сторони АО і АВ, то .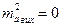

Отже

m_a²=m_b²

або

m_a=m_b.

Формула (2.14) приймає вигляд

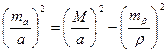
(2.15)

Згідно з Інструкцією [1], відносна помилка визначення сторони не повинна перевищувати

в 4 класі — 1:50000;

в 1 розряді — 1:20000;

в 2 розряді — 1:10000.

2.1.3.3 Оцінка запроектованого ряду

Якщо геодезична мережа запроектована у вигляді ряду трикутників, який опирається на дві вихідні сторони (такий варіант найбільш часто зустрічається в сучасних мережах згущення 1 і 2 розрядів), то оцінка проекту полягає в обчисленні відносної помилки найбільш слабкої сторони ряду (рис. 2.7)

.

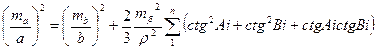(2.16)

Найбільш слабкою стороною ряду є сторона, яка найбільше віддалена від вихідних сторін. Для прикладу на рис. 2.7 приведений ряд тріангуляції 1 розряду, вихідними для якого є сторони тріангуляції 4 класу АС і ВD. найбільш слабкою є сторона тріангуляції 1 розряду KL, віддалена від сторін АС і ВD на 4 трикутники. У формулі (2.16) 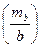— відносна середня квадратична помилка вихідних сторін,

m_b — середня квадратична помилка вимірювання кутів;

Аі, Ві — зв’язуючі кути в трикутниках (кути, які приймають участь в передачі за теоремою синусів сторін від вихідної до найбільш віддаленої, наприклад, для рис. 2.7 — від AC до KL).

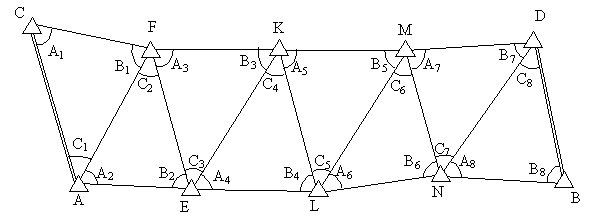
Рисунок 2.7 - Ряд тріангуляції

З рис. 2.7 запишемо

.

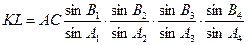(2.17)

Зв’язуючі кути вимірюють транспортиром з карти (в градусах).

У знаку суми , n — кількість трикутників, розміщених між найбільш віддаленою і вихідною сторонами.

Для рис. 2.7 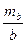слід прийняти 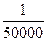, m_b=5'', n=4.

Розрахунок виконують двічі: від двох вихідних сторін. Отримують величини 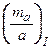і .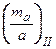

За остаточне значення беруть середнє вагове з двох значень:

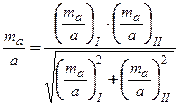
(2.18)

Якщо ця величина не перевищує граничного значення, то роблять висновок, що запроектований ряд трикутників відповідає необхідним технічним вимогам (для вище розглянутого прикладу відносна помилка визначення довжини в найбільш слабкому місці мережі тріангуляції 1 розряду не повинна перевищувати 1:20000).

2.2 Рекогностування пунктів тріангуляції

Рекогностування — це уточнення проекту на місцевості. В результаті рекогностування тріангуляційних пунктів уточнюють остаточні висоти зовнішніх знаків і місця, де будуть закладені пункти тріангуляції. Цю роботу виконує бригада, яку очолює досвідчений інженер-геодезист.

При уточненні висоти сигналу бригада керується тим же основним правилом, що і при проектуванні: між пунктами тріангуляційної мережі, по-перше, повинна бути забезпечена видимість, а, по-друге, висоти знаків повинні бути оптимальними. Вартість побудованих висот знаків на об’єкті буде найменшою, якщо сума їх висот буде мінімальною. Тому завдання бригади при рекогностуванні — розглянути безпосередньо на місцевості усі можливі варіанти, спрямовані на зменшення вартості будівельних робіт. Можливо, з цією метою навіть доведеться змінити місце розташування знаків, а іноді навіть повністю змінити проект.

У залежності від фізико-географічних умов місцевості рекогностування може бути різної складності. Для визначення висоти знаку в деяких випадках достатньо обмежитися простим оглядом місцевості. В інших випадках для цього необхідно виконати додаткові заміри рулеткою або стрічкою. Для цього необхідно піднятися на поруч розміщені споруди: будинки, стовпи, башти, дерева тощо, або в місці розміщення майбутнього знака підняти віхи чи встановити на оточуючих деревах яскраві маркувальні матеріали (марлю, папір, оберемок сіна або соломи тощо). Тому в спорядження бригади мають входити найлегші оптичні прилади (бінокль, технічний теодоліт), мірні засоби (рулетка або стрічка), підіймальні засоби (блоки, троси, канати, вірьовки тощо), засоби підняття на дерева, стовпи, будівлі (кігті, страхувальні пояси, каски та ін.).

Найкраще виконувати рекогностування безпосередньо з будівництвом знаків. Спочатку рекогностувальник встановлює висоти знаків вихідних пунктів, а висоти знаків наступних пунктів визначає, використовуючи побудовані знаки на попередніх пунктах.

Матеріали рекогностування використовуються будівельними бригадами при будівництві знаків.

2.3 Закладання центрів та будівництво зовнішніх знаків

Пункти тріангуляційних мереж закріплюються на місцевості центрами, над якими будуються зовнішні знаки. Центри служать для точного позначення місць розміщення пунктів і довготривалого їх збереження. Зовнішні знаки служать для встановлення на них приладів для спостережень, якщо відсутня видимість пунктів з землі, а також візирних цілей, на які проводяться спостереження з інших пунктів.

2.3.1 Закладання центрів

Типи центрів державних геодезичних мереж регламентуються “Інструкцією про типи центрів геодезичних пунктів” (ГКНТА — 2.01, 02–01–93), ГУГКіК, Київ, 1994 [3].

Для закріплення державних планових мереж застосовуються три види центрів: ґрунтові, скельні та центри на будівлі. Ґрунтові центри застосовуються на місцевості, де відсутнє залягання скелі до поверхні ґрунту ближче 1.8 м. Скельні центри застосовують при близькому заляганні скелі(до 1.8 м). При необхідності розміщення пунктів тріангуляції у містах центри встановлюють на будівлі (як правило, на даху).

Для закріплення пунктів астрономо-геодезичної мережі 1-го класу та геодезичної мережі 2-го класу Інструкція встановлює єдиний тип ґрунтового центру У10П.

Конструкція цього центру приведена на рис. 2.8.

Конструктивно центр складається з п’яти бетонних блоків з трьома металевими марками, що служать охоронними та пізнавальними елементами центра:

- нижній-бетонний куб з стороною 20 см з металевою маркою; об’єм — 0,008 м³, вага — 16 кг;

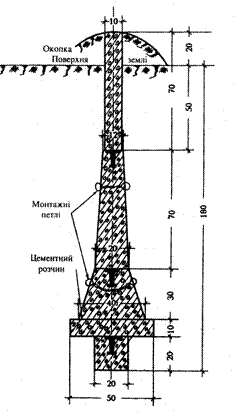
Рисунок 2.8 - Центр пункту тріангуляції, трилатерації, полігонометрії, 1 і 2 класів. Ґрунтовий. Тип У10П

- охоронна плита-бетонна плита 50´50´10 з арматурою із дроту Ø5 мм у вигляді сітки з стороною 10 см та двома монтажними петлями; об’єм — 0,025 м³, вага — 50 кг; верхній — бетонна зрізана піраміда з металевою маркою у верхній площині та монтажними петлями, нижня площина 20´20, верхня 14´14, висота 70 см; об’єм — 0,014 м³, вага — 28 кг;

- пізнавальний стовп — бетонний паралелепіпед 10´10´70; об’єм — 0,007 м³, вага — 14 кг.

Для закріплення пунктів геодезичної мережі 3-го класу Інструкція [3] встановлює тип ґрунтового центру У20П (рис. 2.9).

Центри пунктів тріангуляції, трилатерації, полігонометрії 3 та 4 класів споруджуються із чотирьох бетонних блоків з двома металевими марками:

- нижній — бетонний куб з стороною 20 см з металевою маркою, вага — 16 кг;

- охоронна плита — бетонна плита 50´50´10 з арматурою із дроту Ø5 мм у вигляді сітки з стороною 10 см та двома монтажними петлями, вага — 50 кг;

- верхній — бетонна зрізана піраміда з металевою маркою у верхній площині та монтажними петлями, нижня площина 20´20, верхня 14´14, висота 100 см, вага 40 кг;

- пізнавальний стовп — бетонний паралелепіпед 10´10´70, вага —
14 кг.

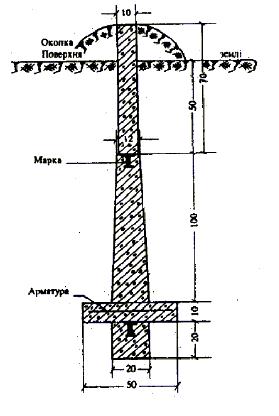
Рисунок 2.9 - Центр пункту тріангуляції, трилатерації, полігонометрії 3, 4 класів. Ґрунтовий. Тип У20П

У випадках близького залягання скелі збирається центр, який вміщує не менше двох блоків з металевими марками з обов’язковим бетонуванням нижнього центра у виїмку, вирубану у скелі, та встановленням на верхньому центрі пізнавального стовпа (тип У30П-при заляганні скелі до 1м, тип 140П – при заляганні скелі від 1 до 1,8 м). Центр типу У30П показаний на рис. 2.10, а типу 140П — на рис. 2.11.

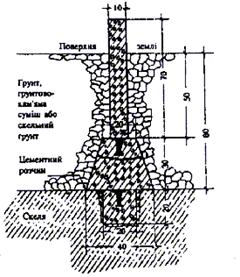
Рисунок. 2.10 - Центр пункту тріангуляції, трилатерації, 1, 2, 3, 4 класів. Скельний. Тип У30П застосовується при заляганні скелі від поверхні землі до 1 м)

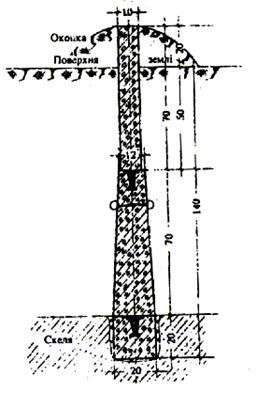
Рисунок 2.11 - Центр пункту тріангуляції, трилатерації, полігонометрії 1, 2, 3, 4 класів.Скельний. Тип 140П
(застосовується при заляганні скелі від поверхні землі від 1м до 1,8м)

Якщо пункт тріангуляції необхідно закріпити на будівлі, застосовують центр типу У16 (рис. 2.12).

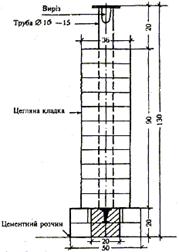
Рисунок 2.12 - Центр пункту тріангуляції, трилатерації, полігонометрії 1, 2, 3, 4 класів на будівлі. Тип У16.

Крім центрів, на кожному пункті планової геодезичної мережі 2 класу необхідно встановити два орієнтирні пункти (ОРП). Їх призначення — служити для азимутальних прив’язок геодезичних мереж нижчого класу в разі, якщо на зовнішній знак, звідки є видимість на суміжні пункти мережі, піднятися немає можливості (підгнили ноги знаку, зруйнована драбина, знак повністю зруйнований тощо); служити для швидкого орієнтування на пункті (наприклад, в разі військових дій), в випадку складних метеорологічних умов (туман, імла, дощ). На центри орієнтирних пунктів має бути видимість як зі столика сигналу, так і з землі.

Закладають ОРП на віддалі 500–1000 м (на забудованій території — не менше 250 м) від пункту тріангуляції. Для полегшення пошуку ОРП закладають так, щоб кут між напрямками на них складав приблизно 90 градусів. Орієнтирному пункту, у якого азимут менший, присвоюють №1, другому — №2.

Для закріплення ОРП на місцевості застосовується центр типу У5
(рис. 2.13).

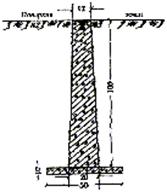
Рисунок 2.13 - Орієнтирний пункт. Тип У5.

На пунктах планової мережі 3 класу ОРП закладаються лише в тому випадку, якщо не забезпечується безпосередньо з землі видимість (земля — земля) між суміжними пунктами мережі.

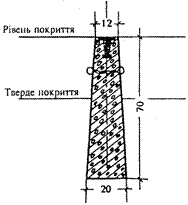
Пункти планових мереж 1 і 2 розрядів закріплюються менш капітальними центрами, висота яких становить 70–75 см. На незабудованих територіях закладають центр типу У15Н. На рис. 2.14. показана конструкція цього центру, розміри, а також форма зовнішнього оформлення у вигляді круглої канави з внутрішнім діаметром 130 см, зовнішнім — 180 см і глибиною 30 см.

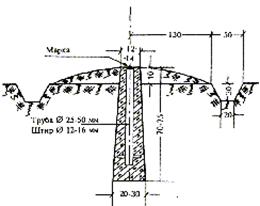
Рисунок 2.14 - Центр пункту планової мережі 1 і 2 розрядів
для незабудованої території. Тип У15Н

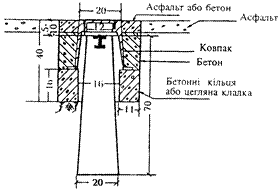
На забудованих територіях закладають центри типу У15, У15К
(рис. 2.15).

а)

б)

Рисунок 2.15 - Центр пункту полігонометрії 1 і 2 розрядів:
а) для територій райцентрів, міст, селищ, сільських населених пунктів (тип У15);
б) для міста Києва, Севастополя та обласних центрів (тип У15к).

Виготовлення центрів здійснюється, як правило, централізованим шляхом за замовленнями геодезичних організацій на заводах залізобетонних конструкцій. При цьому використовуються багатосекційні опалубки, вібратори для ущільнення бетону, бетонозмішувачі та інша техніка.

Закладання центрів здійснюється з допомогою техніки (автоямобурів, екскаваторів) або вручну, із застосуванням найпростіших інструментів.

2.3.2 Будівництво зовнішніх знаків

На пунктах планової геодезичної мережі будують зовнішні знаки таких основних типів:

- піраміда;

- простий сигнал;

- складний сигнал.

Будуються знаки дерев’яні або металічні.

Піраміда будується в тому випадку, коли спостереження на пункті можна виконати зі штатива (рис. 2.16). На пунктах державних мереж 2 і 3 класу будують чотиригранні піраміди, на пунктах мереж згущення 4 класу, 1 і 2 розряду можуть будуватися тригранні піраміди. Висота піраміди 5 –

8 м.

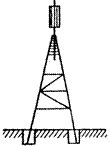
Рисунок 2.16 - Піраміда

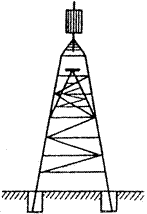
Простий сигнал — це геодезичний знак, який складається з двох пірамід: внутрішньої і зовнішньої. Внутрішня, трикутна піраміда, несе на собі столик для встановлення на ньому приладу (теодоліта, світловіддалеміра тощо). Зовнішня, чотирикутна зрізана піраміда, служить для встановлення на ній площадки для спостерігача та даху з візирною ціллю (рис. 2.17). Піраміди не дотикаються одна до другої.

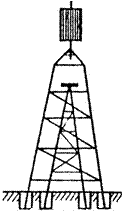
Рисунок 2.17 - Простий сигнал	Рисунок 2.18 - Складний сигнал

Прості сигнали будують у випадках, коли геодезичний прилад треба підняти на висоту від 4 до 10 м.

Складні сигнали будують у тих випадках, коли геодезичний прилад треба підняти на висоту від 11 до 40 м. Складний сигнал складається також з двох пірамід: зовнішньої і внутрішньої, які з’єднані між собою (на відміну від простого сигналу). Зовнішня, трикутна піраміда, несе на собі візирний циліндр, площадку для спостерігача і внутрішню піраміду зі столиком для геодезичного приладу (рис. 2.18).

2.3.3 Зовнішнє оформлення пунктів

Для зовнішнього оформлення пунктів державної геодезичної мережі викопуються канави паралельно до сторін знака. Внутрішній край канави повинен розташовуватись на віддалі 100 см від осей стовпів знака. Ширина канави зверху 120 см, знизу 20 см, глибина — 80 см (рис. 2.19).

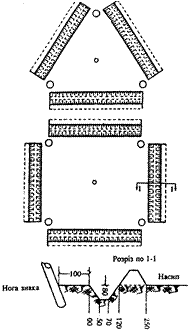
Рисунок 2.19 - Зовнішнє оформлення пунктів тріангуляції 1, 2, 3, 4 класів

Канави викопуються тільки між стовпами, кути знаку не окопуються, щоб можна було підійти до центру пункту. Земля із канави висипається на зовнішню сторону у формі валу.

Пізнавальний стовп центру засипається валом землі для маскування.

У випадку застосування скельного центру типу У30П (скеля підходить до поверхні ґрунту ближче, ніж на 1 м),пункт канавою не окопують.

Зовнішнє оформлення орієнтирних пунктів виконують круглою окопкою шириною 1,0 м зверху, 0,2 м знизу, глибиною 0,5 м (рис. 2.20). Внутрішній діаметр окопки 1,3 м, зовнішній 3,3 м.

У канаві робиться розрив, у якому може встановлюватись розпізнавальний стовп з охоронною пластиною.

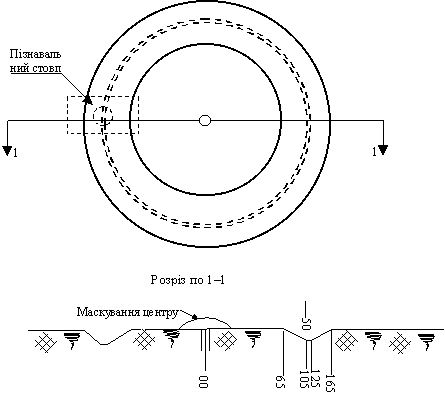
Рисунок 2.20 - Зовнішнє оформлення орієнтирного пункту.

Наступними процесами в технологічній схемі робіт при побудові планових мереж методом тріангуляції є астрономічні спостереження на вихідних пунктах та вимірювання базисів або вихідних сторін. Ці процеси вивчаються у спеціальних курсах “Геодезична астрономія” та “Геодезичні прилади. Розділ: Світло- та радіо-віддалеміри”.

2.4 Кутові спостереження на пунктах тріангуляції і їх попередня обробка

В практиці побудови геодезичних мереж нашої держави застосовувалися чотири способи вимірювання кутів:

- спосіб вимірювання кутів у всіх комбінаціях;

- спосіб кругових заходів;

- видозмінений спосіб вимірювання кутів у всіх комбінаціях;

- спосіб неповних заходів.

2.4.1 Поняття про спосіб вимірювання кутів у всіх комбінаціях

Спосіб вимірювання кутів у всіх комбінаціях був запропонований Гауссом К.Ф. на початку 19 століття. Методичний аспект способу в усіх деталях був розроблений в 70-х роках 19 століття Шрейбером.

Спосіб вимірювання кутів у всіх комбінаціях передбачає вимірювання усіх можливих кутів, які можна скласти з напрямків, що підлягають спостереженню.

Наприклад, якщо на пункті 3 напрямки (рис. 2.21), то в цьому способі вимірюються кути:

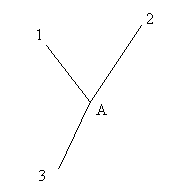
1.2 1.3 2.3

Рисунок 2.21 - Схема вимірювання кутів на пункті А (3 напрямки)

Якщо на пункті 4 напрямки (рис. 2.22), то вимірюються такі кути:

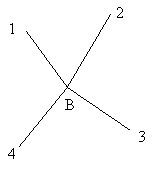
1.2 1.3 1.4 2.3 2.4 3.4

Рисунок 2.22 - Схема вимірювання кутів на пункті В (4 напрямки)

Загальна кількість кутів А, які підлягають вимірюванням, підраховується за формулою

,

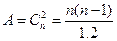(2.19)

де 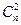— кількість комбінацій, які можна скласти з n напрямків по 2.

Кількість заходів вимірювання кожного кута обчислюється за формулою

,

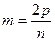(2.20)

де 2 p — вага тріангуляції, яка для тріангуляції 1 класу приймалась 35 або 36, а для тріангуляції 2 класу 28, 30 або 32.

Зауважимо, що величина 2 p = mn завжди постійна, в зв’язку з чим кути, які отримують, будуть рівноточні.

Спосіб вважається самим точним, тому своє основне практичне застосування спосіб знайшов при побудові тріангуляційних мереж 1-го класу. Застосовувався спосіб і при побудові тріангуляційних мереж 2-го класу, але рідше в зв’язку з його громіздкістю, що полягає у великій кількості кутів, які необхідно виміряти у разі великої кількості напрямків (наприклад, при n =9 ).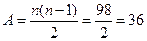

2.4.2 Спосіб кругових заходів

Цей спосіб був запропонований в середині 19 століття російським ученим Струве В.Я. Це найбільш простий за методикою вимірювань і методикою обробки спосіб. Застосовується для 2-го вимірювання напрямків на пунктах 2-го і усіх наступних класів і розрядів тріангуляції, кількість напрямків на яких три і більше.

2.4.2.1 Кількість заходів вимірювання напрямків

Кількість заходів вимірювання напрямків залежить від класу або розряду тріангуляції і точності теодоліта, яким вони вимірюються (табл.2.1)

Таблиця 2.1 - Кількість заходів вимірювання напрямків в тріангуляції

Клас або розряд тріангуляції	Точність теодоліта
0,5″	1″	2″	5″
2 клас				—
3 клас				—
4 клас	—			—
1 розряд	—
2 розряд	—

2.4.2.2 Величина, на яку переставляється лімб між заходами

Між заходами лімб переставляється на величину

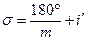
(2.21)

або

,

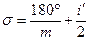(2.21′)

де m — кількість заходів,

i — ціна ділення лімба теодоліта.

З використанням величини s обчислюють установки лімба на початковий напрямок для кожного заходу спостережень. За початковий обирають напрямок з найкращими умовами спостережень.

В першому заході установка лімба на початковий напрямок повинна становити 0º0′, в кожному наступному лімб переставляється на величину s, обчислену за формулою (2.21) або (2.21′).

Наприклад, кути вимірюються на пункті тріангуляції 3 класу теодолітом 2Т2 9-ма заходами. Тоді за формулою (2.21′)

.

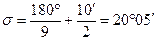Установки лімба при наведенні на початковий напрямок приведені в
табл. 2.2.

Таблиця 2.2 - Установки лімба для теодоліта 2Т2 в тріангуляції 3 класу

Номер заходу	Установка лімба
	0º 0′
	20 05
	40 10
	60 15
	80 20
	100 25
	120 30
	140 35
	160 40

Методика встановлення установки лімба для різних типів теодолітів вивчається в курсі “Геодезичні прилади”.

2.4.2.3 Приведення приладів в робоче положення

Перед вимірюванням напрямків встановлюють теодоліт над центром пункту, центрують з допомогою оптичного виска і приводять вісь обертання теодоліта в прямовисне положення з допомогою рівня при алідаді горизонтального круга (горизонтують прилад). При нівелюванні приладу центр оптичного виска зійде з зображення центру пункту. Тому рекомендується ці операції виконувати в такій послідовності:

1) встановити трегер з теодолітом всередині головки штатива, а усі підйомні гвинти вивести в середнє положення;

2) спостерігаючи в окуляр оптичного виска, встановити якнайточніше штатив з теодолітом над точкою;

3) почергово встановлюючи циліндричний рівень в напрямку кожної з ніжок штатива, вивести його з допомогою ніжок (піднімаючи або опускаючи їх) на середину (тобто відгоризонтувати прилад);

4) підправити (за необхідністю) горизонтування приладу з допомогою підйомних гвинтів трегера;

5) підправити центрування теодоліта переміщенням трегера на головці штатива (попередньо відкріпивши становий гвинт).

Після цього наводять теодоліт на початковий напрямок і встановлюють на лімбі відлік 0º0′ (у першому заході).

З метою уникнення можливих деформацій штатива і теодоліта, захищають їх від сонця геодезичною парасолею.

2.4.2.4 Методика наведення теодоліта на візирну ціль і взяття відліків

Перед тим, як описати методику вимірювання напрямків способом кругових заходів, встановимо, як здійснюється наведення теодоліта на візирну ціль і взяття відліків. Ця операція здійснюється так: плавним рухом алідада відводиться вліво від візирної цілі на 30–40º, потім різким рухом вправо наводиться приблизно на візирну ціль і закріплюється закріпним гвинтом.

Що означає “приблизно навести на візирну ціль”?

Візирна вісь при одному крузі трохи не доводиться до візирної цілі, при іншому — переводиться за неї. В цьому випадку остаточне наведення візирної осі на центр візирної цілі здійснюється мікрометреним гвинтом за ходом годинникової стрілки.

Після остаточного наведення візирної осі на центр візирної цілі береться двічі відлік на горизонтальному крузі. В теодолітах 5″-ої точності він береться простим відрахуванням на шкалі горизонтального круга. Для того, щоб відлік взяти вдруге, необхідно рухом мікрометреного гвинта алідади на 0.5–1 оберт проти годинникової стрілки трохи змістити візирну вісь з центра візирної цілі і знову навести на її центр, закінчуючи рух мікрометреного гвинта за годинниковою стрілкою.

У теодолітах 2″-ої точності відлік береться суміщенням зображень штрихів протилежних країв лімба, яке необхідно завершувати обертанням барабанчика оптичного мікрометра за ходом годинникової стрілки. Щоб відлік взяти двічі, цю операцію треба повторити двічі при одному і тому ж наведенні візирної труби теодоліта на центр візирної цілі.

2.4.2.5 Методика вимірювання напрямків

Тепер розглянемо методику вимірювання напрямків в одному заході. Нехай на пункті А вимірюється n напрямків (рис. 2.23).

Вимірювання кута в одному заході виконується двома півзаходами.

Перший півзахід розпочинається зі встановлення на лімбі установки, обчисленої для початкового напрямку в даному заході.

Далі виконуються почергові наведення труби при КЛ на усі напрямки, починаючи з 1-го (початкового) за годинниковою стрілкою і взяття відліків двічі на кожний напрямок. Завершується півзахід повторним наведенням на 1-й (початковий) напрямок і взяттям відліків (двічі). Різниця між середніми відліками в кінці і на початку півзаходу носить назву “незамикання горизонту”. Його допустимі значення приведені в табл. 2.3.

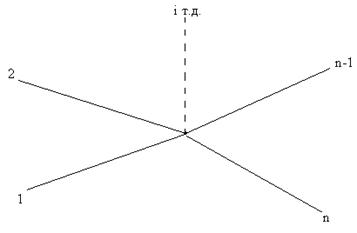
Рисунок 2.23 - Схема вимірювання кутів на пункті А способом кругових заходів

Таблиця 2.3 - Допуски при вимірюванні напрямків способом кругових заходів

Назви допуску	Величина допуску при вимірюванні теодолітами точності
1″	2″	5″
Незамикання горизонту в одному півзаході	6″	8″	0′,2
Коливання 2 с в одному заході	9″	12″	0′,3
Коливання між заходами напрямків, приведених до нуля	5″	8″	0′,2

Другий півзахід виконується почерговими наведеннями труби при КП на усі напрямки, починаючи з 1-го, проти годинникової стрілки і взяттям відліків двічі на кожний напрямок. Завершується півзахід повторним наведенням на 1-й напрямок, взяттям відліків і обчисленням “не замикання горизонту”, яке не повинно перевищувати допустимих значень.

Перед початком кожного півзаходу рекомендується алідаду кілька разів обернути в напрямку її наступного руху в даному півзаході.

Обробка результатів спостережень виконується в такій послідовності.

Якщо в першому півзаході при КЛ отримані середні відліки на напрямки

L ₁, L ₂, …, L_n, L ₁′,

а при КП

R ₁, R ₂,…, Rn, R ₁′,

то середні напрямки, обчислені з вимірів при двох кругах, обчислюють за формулою

.

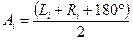(2.22)

При вимірюваннях обчислюють подвійну колімаційну помилку на усі напрямки за формулою

.

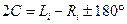(2.23)

Контролюється її зміна в межах одного заходу (табл.2.3).

Незамикання горизонту обчислюють так:

при КЛ

D L = L 1^/– L 1,

(2.24)

при КП

D R=R 1^/– R 1.

(2.24¢)

Середнє незамикання

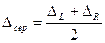
(2.25)

необхідно розподілити в середні напрямки за формулою:

,

(2.26

де d_i — поправка у відповідний напрямок,

n — кількість напрямків на пункті,

i — номер напрямку.

Після цього обчислюють напрямки, виправлені за незамикання горизонту

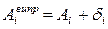
(2.27)

і напрямки приведені до початкового (до нуля):

.

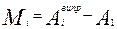(2.28)

У табл. 2.3 приведені граничні коливання між заходами напрямків, приведених до нуля.

2.4.3 Поняття про видозмінений спосіб вимірювання кутів у всіх комбінаціях

Для скорочення обсягів польових спостережень, в 1950 р. радянським інженером-геодезистом Томіліним А.Ф. був запропонований видозмінений спосіб вимірювання кутів у всіх комбінаціях для пунктів з 6 і більше напрямками. У цьому способі вимірюються всі кути, які утворюються парою суміжних напрямків і кути утворені парою напрямків з пропуском напрямку, що лежить між ними. Наприклад, на пункті з 7 напрямків (рис. 2.24) вимірюють такі кути:

1.2 2.3 3.4 4.5 5.6 6.7 7.1

1.3 2.4 3.5 4.6 5.7 6.1 7.2

Кількість виміряних кутів на станції завжди буде 2 n.

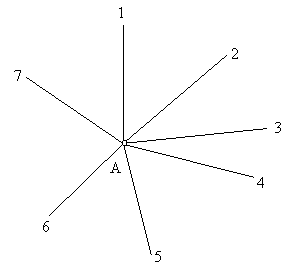
Рисунок 2.24 - Схема вимірювання кутів у видозміненому способі у всіх комбінаціях

2.4.4 Поняття про спосіб неповних заходів

Для скорочення обсягів спостережень на пункті в 1954р. радянським інженером Аладжаловим Ю.А. запропонований спосіб неповних заходів вимірювання кутів на пунктах тріангуляції з 7–9 напрямків. У цьому способі вимірюються кути групами з 3 напрямків. Ці групи сформовані так, щоб були виміряні усі кути, які належало би виміряти способом в усіх комбінаціях. Наприклад на пункті тріангуляції з 7 напрямків це будуть такі групи:

1.2.3.

2.4.5.

3.5.7.

3.4.6.

5.6.1.

6.7.2.

4.7.1.

Для порівняння приведемо кути, які треба було б виміряти способом в усіх комбінаціях:

1.2 1.3 1.4 1.5 1.6 1.7 2.3 2.4 2.5 2.6 2.7 3.4 3.5 3.6 3.7 4.5 4.6 4.7 5.6 5.7 6.7

Кожен з цих кутів або його доповнення до 360º знаходиться в одній із груп з 3-х напрямків.

2.4.5 Приведення результатів кутових вимірів до центрів пунктів

В результаті кутових спостережень в тріангуляції повинні бути виміряні значення напрямків, які з’єднують центри пунктів. Проте, виміряти безпосередньо вказані напрямки немає можливості, оскільки теодоліт не завжди вдається встановити над центром, а візирні циліндри, на які виконуються спостереження, у більшості випадків мають деяке зміщення у відношенні до центрів пунктів.

Тому, щоб отримати напрямки, приведені до центрів пунктів, у виміряні напрямки необхідно ввести поправки за позацентрове встановлення теодоліта і за відхилення візирної цілі. Напрямки, виправлені за центрування теодоліта і за редукцію візирного циліндра, називаються напрямками приведеними до центрів пунктів.

Щоб обчислити вказані поправки, на кожному пункті необхідно визначити так звані елементи приведення, а саме — елементи центрування і елементи редукції.

Розглянемо ці елементи і їх вплив на виміряні напрямки.

2.4.5.1 Елементи центрування і редукції

Якщо проекція центру приладу І не співпадає з центром С пункту (рис. 2.25), то l=ІС — лінійний елемент центрування, θ — кутовий елемент центрування на пункт 1 (кут, виміряний за годинниковою стрілкою в т. І від напрямку на центр С до напрямку на пункт 1).

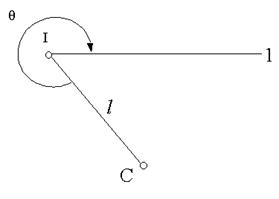
Рисунок 2.25 - Елементи центрування

Якщо проекція візирного циліндра V не співпадає з центром С пункту (рис. 2.26), то l ₁= VC — лінійний елемент редукції, θ ₁ — кутовий елемент редукції для пункту 1 (кут, виміряний за годинниковою стрілкою в точці V від напрямку на центр C до напрямку на пункт 1).

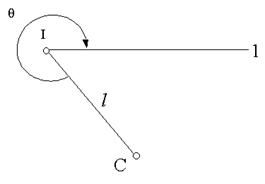
Рисунок 2.26 - Елементи редукції

2.4.5.2 Обчислення поправок у виміряні напрямки за центрування

Розглянемо рис. 2.27, на якому в т. С (центр пункту) зображено 3 напрямки (1, 2, 3), які підлягають спостереженням. В дійсності ці напрямки спостерігаються з т. І стояння теодоліта.

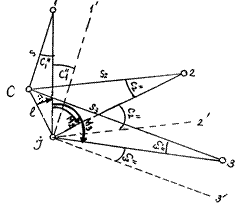
Рисунок 2.27 - Поправки у виміряні напрямки за центрування

Напрямок 1 — початковий.

Кут між 1-м і 2-м напрямком позначимо М ₂, між 1-м і 3-м — М ₃. Лінійний елемент центрування l=CІ. Кутові елементи центрування:

для пункту 1 — θ,

для пункту 2 — θ + М ₂,

для пункту 3 — θ + М ₃.

Поправка за центрування у виміряний напрямок I 1 графічно виражається кутом 1 I 1′, між напрямками І 1 і І 1, який є паралельним до С 1. З рисунка бачимо, що Ð 1І1 ′ = Ð С1І як кути при відрізку 1 І, що пересікається двома паралельними прямими.

З Δ С 1 І бачимо, що

,

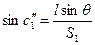або враховуючи мале значення 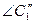, маємо

.

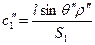(2.29)

За формулою (2.24) обчислюють поправку за центрування в початковий напрямок 1.

Міркуючи аналогічно, отримуємо формули для обчислення поправок за центрування в напрямки 2 і 3.

З Δ С 2 І

,

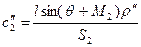(2.29′)

З Δ С 3 І

.

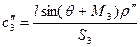(2.29″)

2.4.5.3 Обчислення поправок у виміряні напрямки за редукцію

Розглянемо рис. 2.28, на якому С — проекція на площину центру пункту, на який ведуться спостереження з пунктів 1, 2, 3; V — проекція на цю ж площину візирного циліндра.

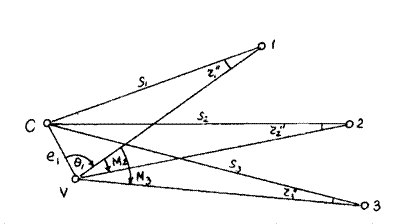
Рисунок 2.28 - Поправка у виміряні напрямки за редукцією

Тут l ₁= VC — лінійний елемент редукції,

θ₁ — кутовий елемент редукції для пункту 1,

θ₁+ M ₂ — кутовий елемент редукції для пункту 2,

θ₁+ М ₃ — кутовий елемент редукції для пункту 3.

Поправка за редукцію у напрямок, виміряний з пункту 1, графічно виражається кутом r ₁, з пункту 2 — r ₂, з пункту 3 — r ₃.

З ∆ СV 1

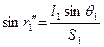
або

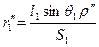
(2.30)

Аналогічно

з ∆ СV 2

(2.30′)

з ∆ СV 3

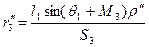
(2.30″)

2.4.5.4 Визначення елементів приведення

Як правило, елементи приведення визначають графічним методом з використанням технічного теодоліта і центрувального столика.

Визначення виконують двічі: до спостережень і після спостережень.

Центрувальний столик з прикріпленим до нього листом ватману або іншого паперу являє собою площину, на яку проектують центр пункту, центр приладу і центр візирного циліндра (рис. 2.29).

Для цього над центром пункту встановлюють центрувальний столик, приводять його в горизонтальне положення і кнопками прикріплюють до нього центрувальний лист таким чином, щоб на нього проектувались центр пункту С, вісь приладу І і візирна ціль V. Ці точки проектують на центрувальний лист з трьох станцій, напрямки на які з центра пункту складали б між собою кути близькі до 120º або 60º. Віддалі від станцій до центра пункту повинні дорівнювати подвійній висоті знака.

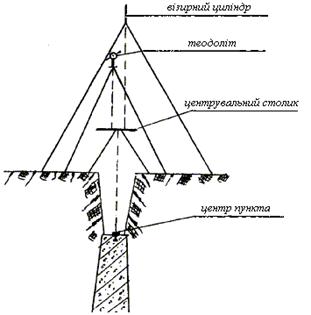
Рисунок 2.29 - Графічний метод визначення елементів приведення

Проектування виконують перевіреним і приведеним в робочий стан технічним теодолітом. При цьому спостерігач спочатку при крузі ліво наводить сітку ниток на центр пункту, піднімає трубу так, щоб її поле зору попадало на планшет. Помічник за вказівкою спостерігача позначає на двох протилежних кінцях центрувального листа дві точки С ₁, які визначають напрямок зі станції на центр пункту при крузі ліво.

Аналогічно проектують на центрувальний столик вісь обертання приладу і позначають дві точки і ₁, потім проектують вісь симетрії візирного циліндра і отримують дві точки v ₁. Повторюють всі операції при крузі право і поруч з кожною точкою с ₁, і ₁, v ₁ отримують ще по одній точці (їх не підписують, лише позначають).

Таким чином, на першій станції теодоліта отримали шість пар точок: по дві пари с ₁, і ₁, v ₁ (рис. 2.30).

Прокресливши рискою в кожній парі точок середину між ними і з’єднавши їх, отримують напрямки на центр с ₁ с ₁, вісь приладу і ₁ і ₁, вісь симетрії візирного циліндра v ₁ v ₁.

Переходять з теодолітом на другу станцію. Аналогічно отримують шість пар точок на другій станції: по дві пари c ₂, і ₂, v ₂ (рис. 2.31).

Прокреслюють рискою в кожній парі точок середину між ними і почергово, приклавши до них лінійку, відмічають рискою перетин напрямку і ₂ і ₂ з і ₁ і ₁; напрямку v ₂ v ₂ з v ₁ v ₁.

Переходять з теодолітом на третю станцію. Аналогічно отримують шість пар точок: по дві пари c ₃, і ₃, v ₃.

Аналогічно прокреслюють напрямки c ₃ c ₃, і ₃ і ₃, v ₃ v ₃.

У місцях перетину з відповідними напрямками на двох попередніх станціях отримують трикутники похибок (рис. 2.32), які характеризують якість проектування центру пункту, осі приладу та осі симетрії візирного циліндра на центрувальний лист.

Сторони трикутників похибок не повинні перевищувати 5 мм при проектуванні С та І та 10 мм при проектуванні V.

Якщо ці умови витримані, на око визначають центри ваг трикутників похибок, відмічають їх точками і позначають С, І та V відповідно.

До точки І та V по черзі прикладають візирну або просту лінійку і, провізувавши її на два пункти мережі і два орієнтирні пункти (якщо вони є), проводять на них напрямки, помітивши їх стрілками і підписавши. Якщо з висоти центрувального столика пунктів мережі не видно, то попередньо на їх простецевих (створених) лініях з допомогою теодоліта виставляють тички (віхи), на які й візують лінійки.

Після цього приступають до оформлення центрувального листа. Вимірюють лінійний (лінійкою) та кутовий (транспортиром) елементи центрування, лінійний та кутовий елементи редукції, записують їх.

Контроль кутових елементів центрування θ і редукції θ ₁ здійснюють за контрольними кутами на прокреслені напрямки пунктів мережі чи орієнтирних пунктів. Графічні значення цих кутів не повинні відрізнятися від виміряних більше ніж на 2º при l і l ₁ менших 10 мм, 1º — при l і l ₁ від 10 до 20 мм і 0,5 при l і l ₁ більших 20 мм.

Як вже вказувалось, визначення елементів приведення виконують двічі: до вимірювання горизонтальних кутів і після їх вимірювання.

Після повторного визначення порівнюють значення l і l ₁ з відповідними значеннями до спостережень. Вони не повинні відрізнятися більше як на 10 мм. Якщо ця умова витримана, за останнє приймають середнє значення. В протилежному випадку виконують третє визначення. Якщо його значення співпадає з першим, тоді друге вважається помилковим, якщо з другим — вважають, що відбулися зміни у положенні C, І, V за час, що пройшов між першим і повторним визначенням елементів приведення. В цьому випадку необхідно проаналізувати результати кутових вимірів і прийняти правильне рішення, які результати визначення елементів приведення прийняти за остаточні для введення поправок у виміряні напрямки.

Дата добавления: 2014-01-05