
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Э л л и п с
|
|
|
|
Эллипс - геометрическое место точек на плоскости, для каждой из которых сумма расстояний до двух данных точек F1 и F2 той же плоскости, называемых фокусами эллипса, есть величина постоянная, равная 2а и большая, чем расстояние между фокусами 2с.
Выведем уравнение эллипса, исходя из данного определения.
Выберем систему координат так, чтобы ось абсцисс проходила через фокусы эллипса F1 и F2. Ось ординат проведем через середину отрезка перпендикулярно F1 F2 ему.

| Пусть M(x,y) - произвольная точка эллипса. Расстояния от любой точки M(x,y) эллипса до фокусов называются ее фокальными радиусами. r1 =F1M; r2=F2M – фокальные радиусы. Согласно определению эллипса сумма F1M+F2M=2a. |
Тогда координаты точек эллипса удовлетворяют уравнению
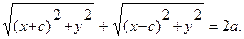
Уединяя один из радикалов, возводим обе части уравнения в квадрат:
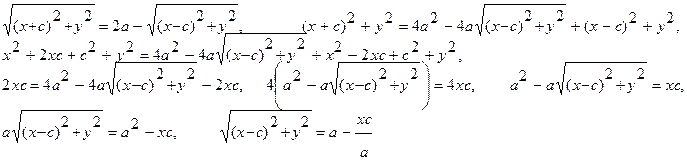 Снова возведем обе части уравнения в квадрат и приведем подобные члены:
Снова возведем обе части уравнения в квадрат и приведем подобные члены:
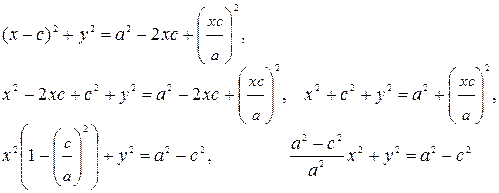
По определению эллипса 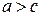 , поэтому
, поэтому  – положительное число. Обозначим его через
– положительное число. Обозначим его через  , положим
, положим 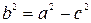 , т.е.
, т.е. 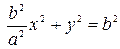 . После деления на
. После деления на  уравнение примет вид:
уравнение примет вид:

Это уравнение называется каноническим уравнением эллипса.
Из уравнения 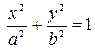 видно, что эллипс симметричен относительно осей OX, OY и начала координат, так как вместе с точкой (x,y) ему принадлежат и точки (-x,-y), (-x, y), (x, -y). Эллипс пересекает оси координат в точках А (а;0), С(-а;0) (это точки пересечения с осью OX), В(0;b), D(0;-b) (это точки пересечения о осью OY). Точки пересечения с осями координат называются вершинами эллипса. Отрезок АС называется большой осью эллипса, отрезок BD – малой осью. Длина большой оси равна 2а, длина малой оси равна 2b. Числа а и b называют полуосями эллипса.
видно, что эллипс симметричен относительно осей OX, OY и начала координат, так как вместе с точкой (x,y) ему принадлежат и точки (-x,-y), (-x, y), (x, -y). Эллипс пересекает оси координат в точках А (а;0), С(-а;0) (это точки пересечения с осью OX), В(0;b), D(0;-b) (это точки пересечения о осью OY). Точки пересечения с осями координат называются вершинами эллипса. Отрезок АС называется большой осью эллипса, отрезок BD – малой осью. Длина большой оси равна 2а, длина малой оси равна 2b. Числа а и b называют полуосями эллипса.
Из уравнения 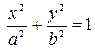 следует, что каждое слагаемое в левой части не превосходит единицы, т.е. имеют место неравенства:
следует, что каждое слагаемое в левой части не превосходит единицы, т.е. имеют место неравенства: 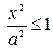 и
и  или
или 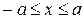 и
и  . Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми
. Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми 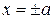 и
и  . В каноническом уравнении эллипса сумма неотрицательных слагаемых
. В каноническом уравнении эллипса сумма неотрицательных слагаемых 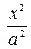 и
и 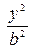 равна 1. При возрастании одного слагаемого, другое будет уменьшаться, т.е. если
равна 1. При возрастании одного слагаемого, другое будет уменьшаться, т.е. если  возрастает, то
возрастает, то  уменьшается и наоборот. Значит, эллипс имеет форму, изображенную на рисунке (овальная замкнутая кривая).
уменьшается и наоборот. Значит, эллипс имеет форму, изображенную на рисунке (овальная замкнутая кривая).

| Точки А,С, В,D –вершины эллипса. АС=2а – большая ось эллипса, BD=2b – малая ось эллипса, АО=а – большая полуось эллипса, ОВ=b – малая полуось эллипса. F1M и F2M – фокальные радиусы. |
Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси. Обозначив эксцентриситет через 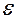 , получим
, получим 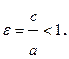 Эксцентриситет характеризует вытянутость эллипса, так как выражается через отношение его полуосей:
Эксцентриситет характеризует вытянутость эллипса, так как выражается через отношение его полуосей: 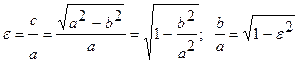 . Отсюда видно, что чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным; если положить
. Отсюда видно, что чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным; если положить  , то эллипс превращается в окружность.
, то эллипс превращается в окружность.
Для произвольной точки М(х,у), принадлежащей эллипсу верны соотношения:
 и
и 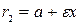 .
.
С эллипсом связаны две прямые, называемые директрисами. Их уравнения:
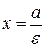 и
и 
Если r – расстояние от произвольной точки эллипса до какого-нибудь фокуса F, d – расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение 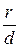 есть постоянная величина, равная эксцентриситету эллипса:
есть постоянная величина, равная эксцентриситету эллипса:  .
.

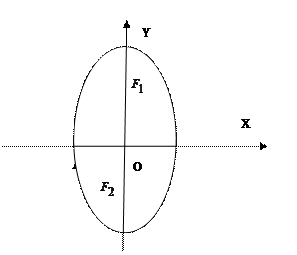
Из равенства 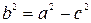 следует, что следует, что  . Если же . Если же 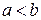 , то уравнение , то уравнение 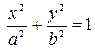 определяет эллипс, большая ось которого 2b лежит на оси Оу, а малая ось 2а – на оси Ох. Фокусы такого эллипса находятся в точках определяет эллипс, большая ось которого 2b лежит на оси Оу, а малая ось 2а – на оси Ох. Фокусы такого эллипса находятся в точках 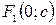 и и  , где , где  . .
| 
|
Пример 1. Доказать, что уравнение 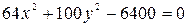 является уравнением эллипса. Найти координаты фокусов и фокальное расстояние.
является уравнением эллипса. Найти координаты фокусов и фокальное расстояние.
Разделив обе части уравнения на 6400, получим: 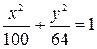 . Это уравнение является каноническим уравнением эллипса. Из равенства
. Это уравнение является каноническим уравнением эллипса. Из равенства 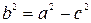 следует, что
следует, что  и с=6. Фокусы эллипса будут находиться в точках
и с=6. Фокусы эллипса будут находиться в точках 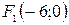 и
и 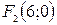 . Фокальное расстояние
. Фокальное расстояние 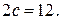
Пример 3. Составить уравнение эллипса, если его фокусы F1(0; 0), F2(1; 1), большая ось равна 2.
Уравнение эллипса имеет вид: 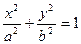 . Расстояние между фокусами:
. Расстояние между фокусами:
2c =  , таким образом, a2 – b2 = c2 = ½. По условию 2а = 2, следовательно а = 1, b =
, таким образом, a2 – b2 = c2 = ½. По условию 2а = 2, следовательно а = 1, b = 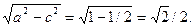 Итого:
Итого: 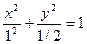 .
.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 558; Нарушение авторских прав?; Мы поможем в написании вашей работы!